Attention in Transformers - 3Blue1Brown
3Blue1Brown Infographic Summary
Table of Contents
- Exploring the Attention Mechanism in Transformers | 0:00:00-0:04:00
- The Attention Block | 0:04:00-0:09:00
- The Attention Mechanism in Transformers | 0:09:00-0:20:20
- Multi-Headed Attention in GPT-3 | 0:20:20-10:10:10
Exploring the Attention Mechanism in Transformers | 0:00:00-0:04:00
https://youtu.be/eMlx5fFNoYc?t=0
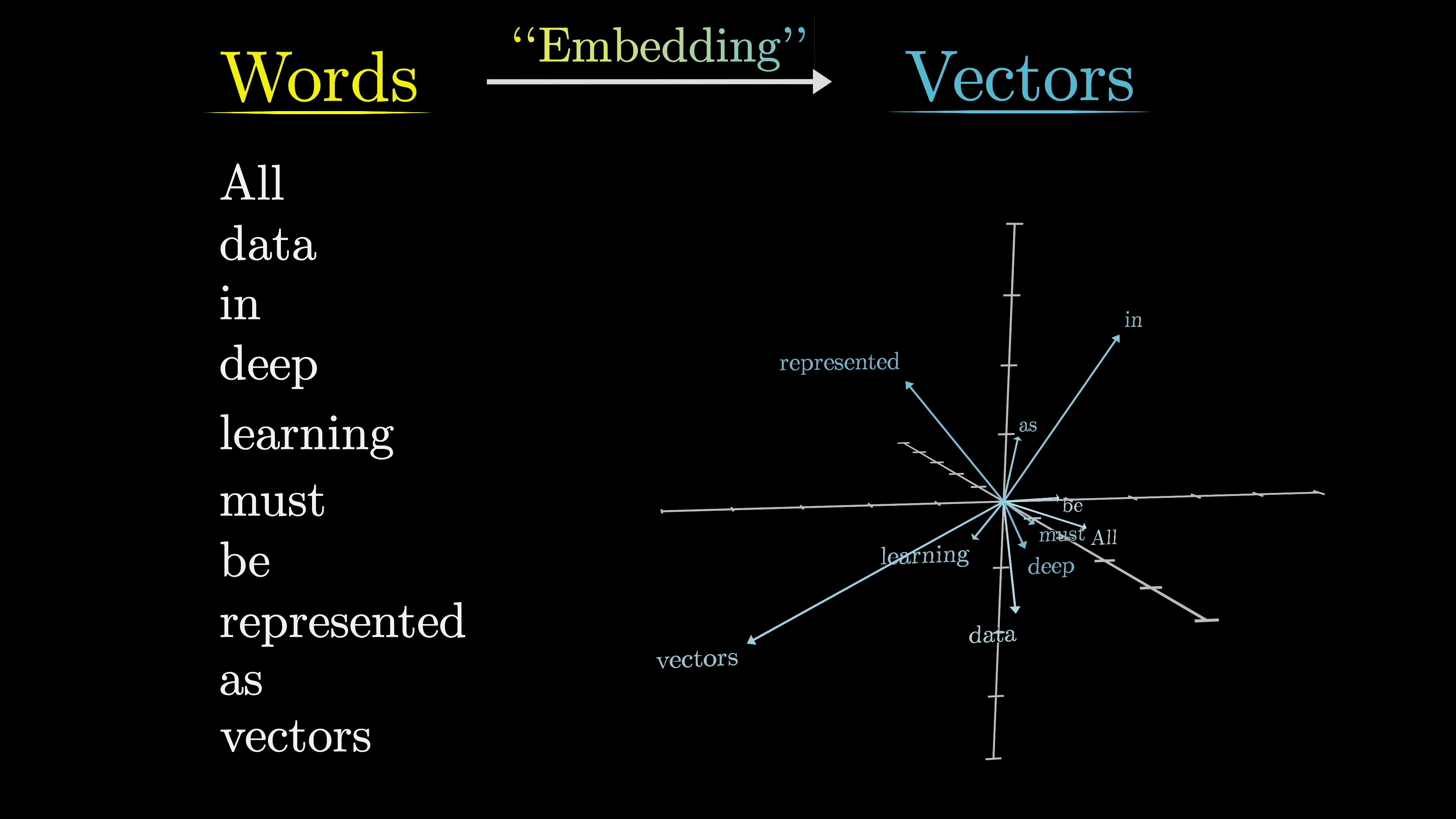
Tokens, which are smaller units of text, are associated with high-dimensional vectors called embeddings.

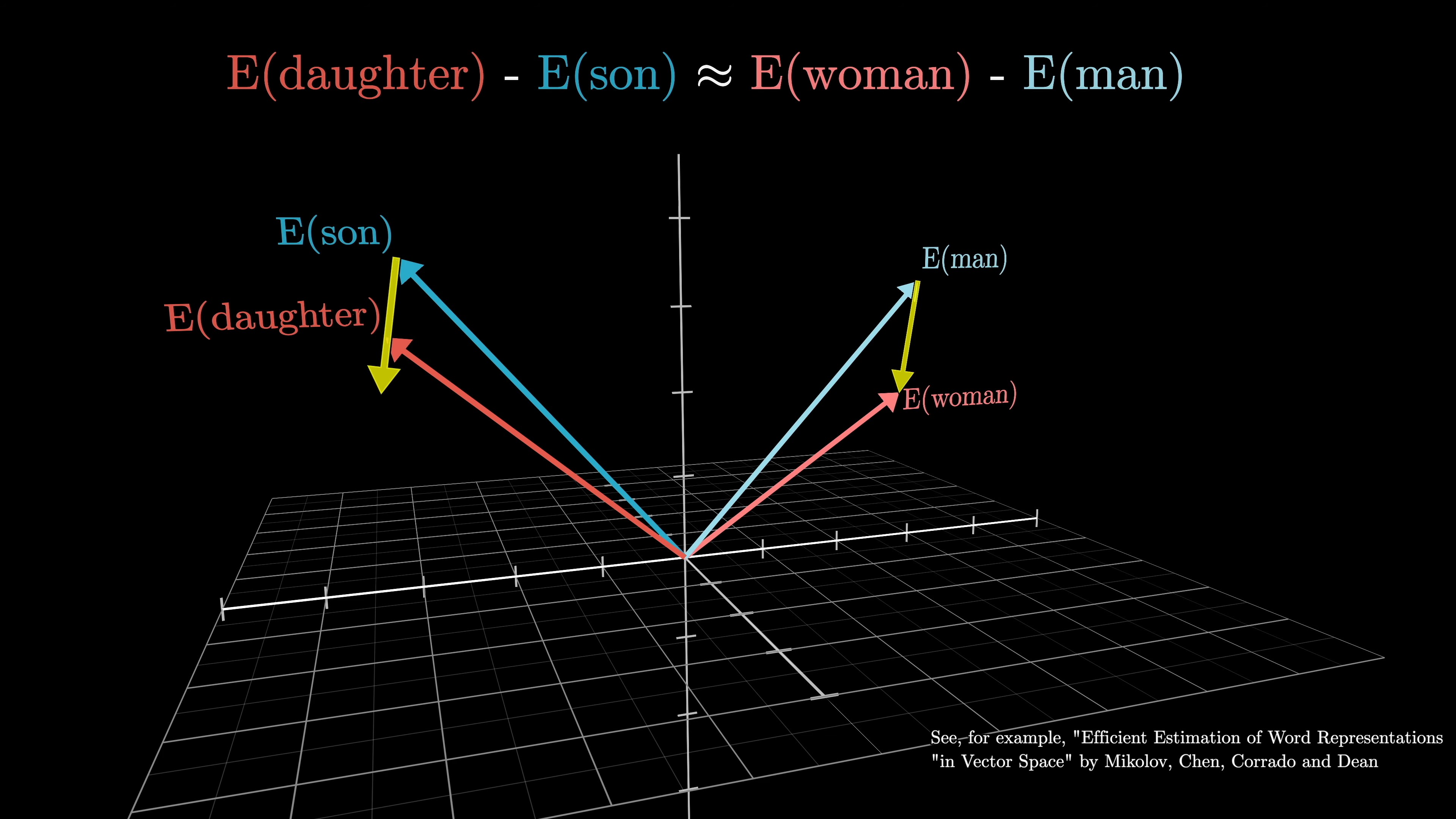
These embeddings capture semantic meaning in the high-dimensional space.

The attention mechanism helps adjust these embeddings to encode richer contextual meaning. Many people find the attention mechanism complex, but it is a crucial component in language models and AI tools.
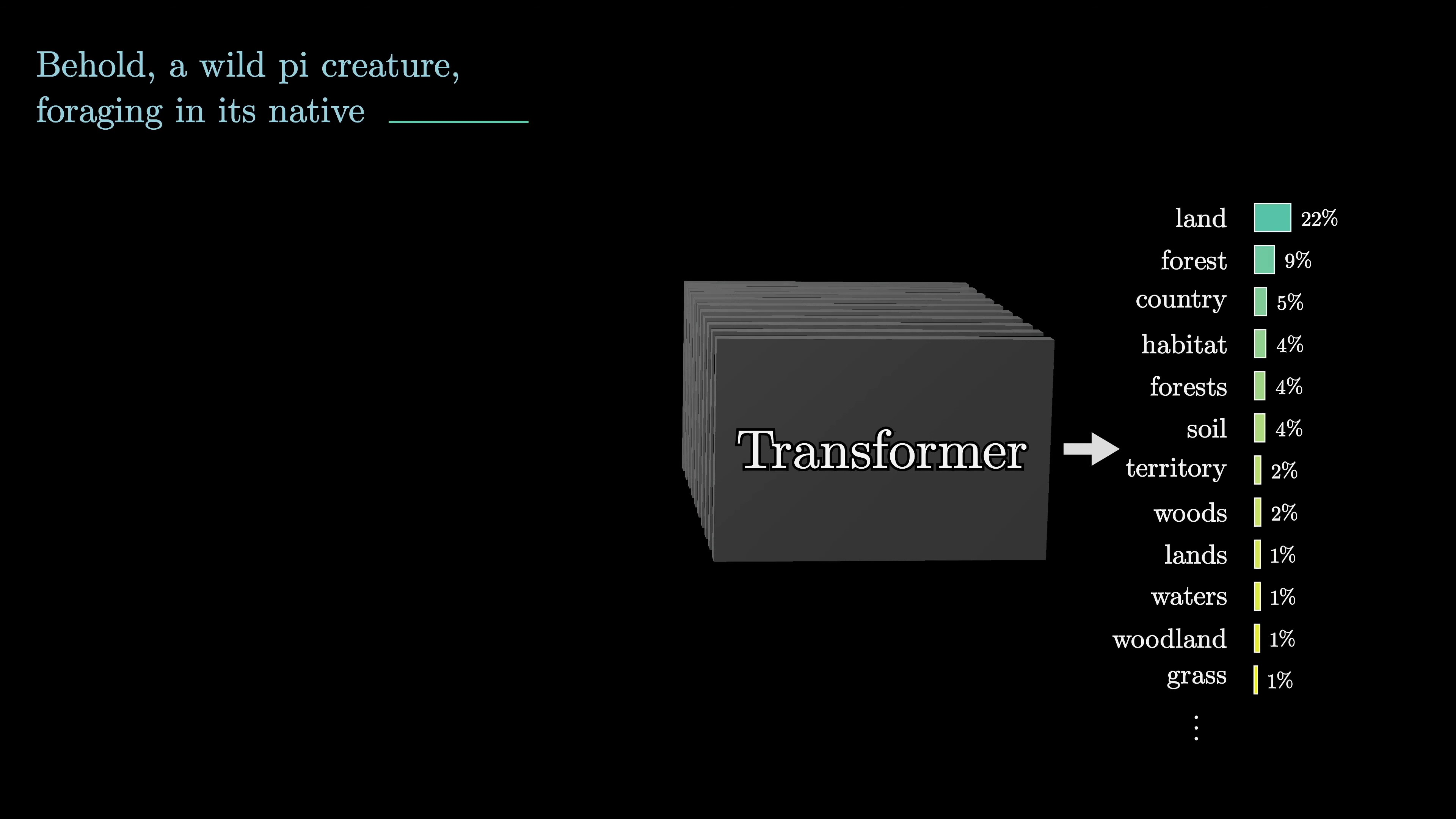
Before diving into the computational details of the transformer's key piece, it's helpful to consider an example that demonstrates the desired behavior of attention.
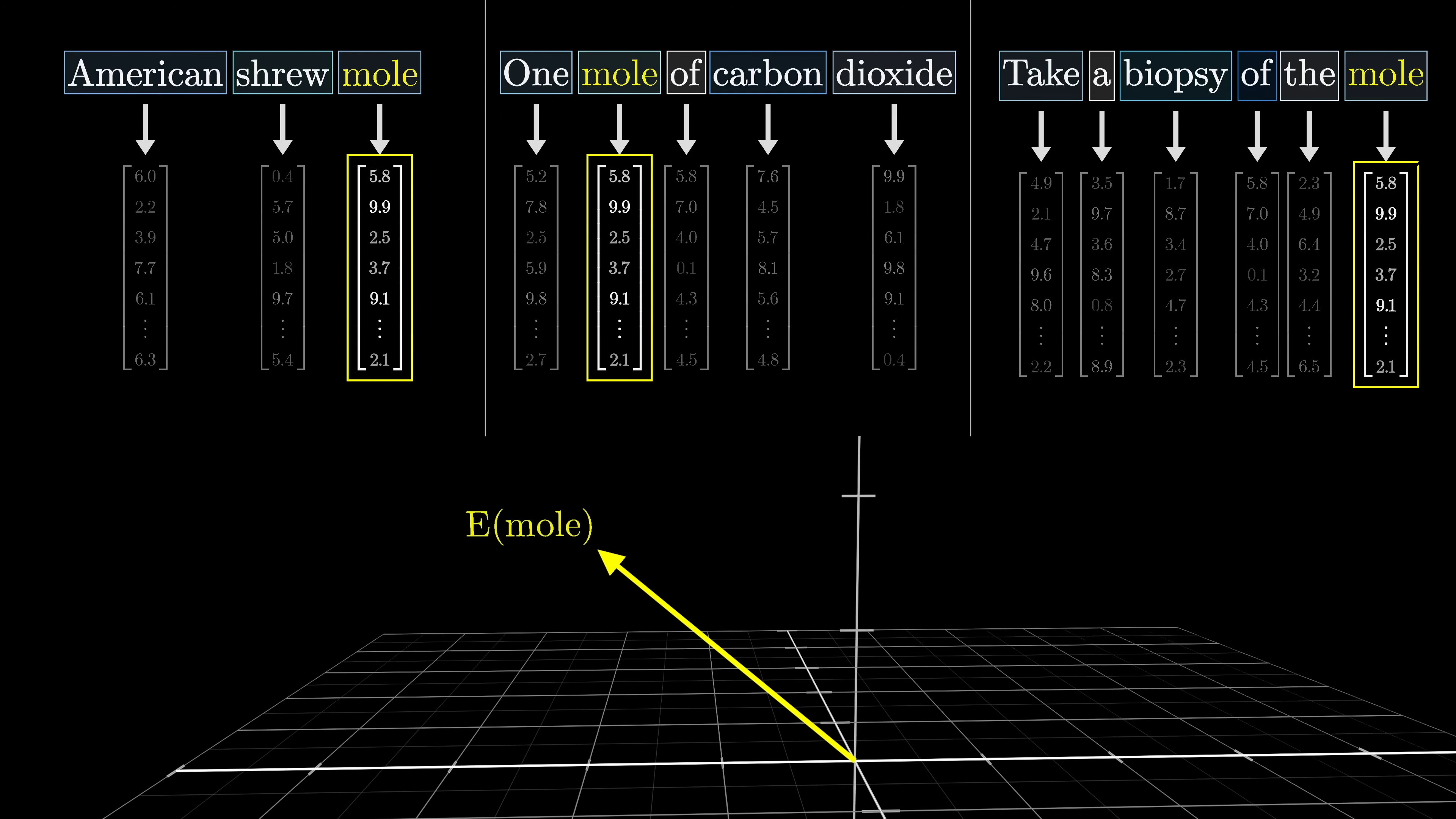
The word 'mole' has different meanings in different contexts, but in the initial step of a transformer, the vector associated with 'mole' is the same in all cases. It's in the next step that the surrounding embeddings provide context and influence the specific meaning. The attention block allows the model to refine the meaning of a word and transfer information between embeddings. The prediction of the next token is based on the last vector in the sequence.
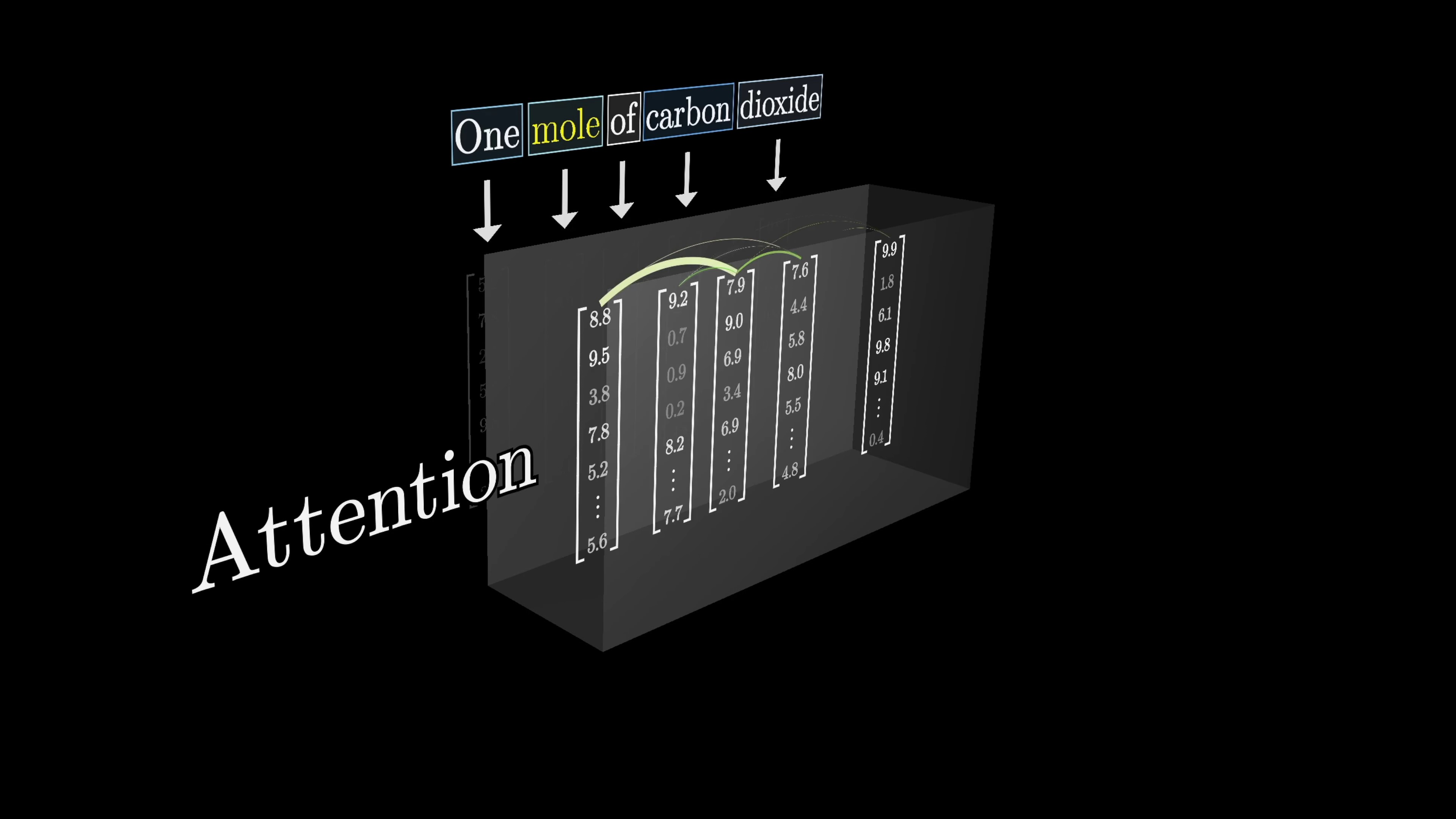

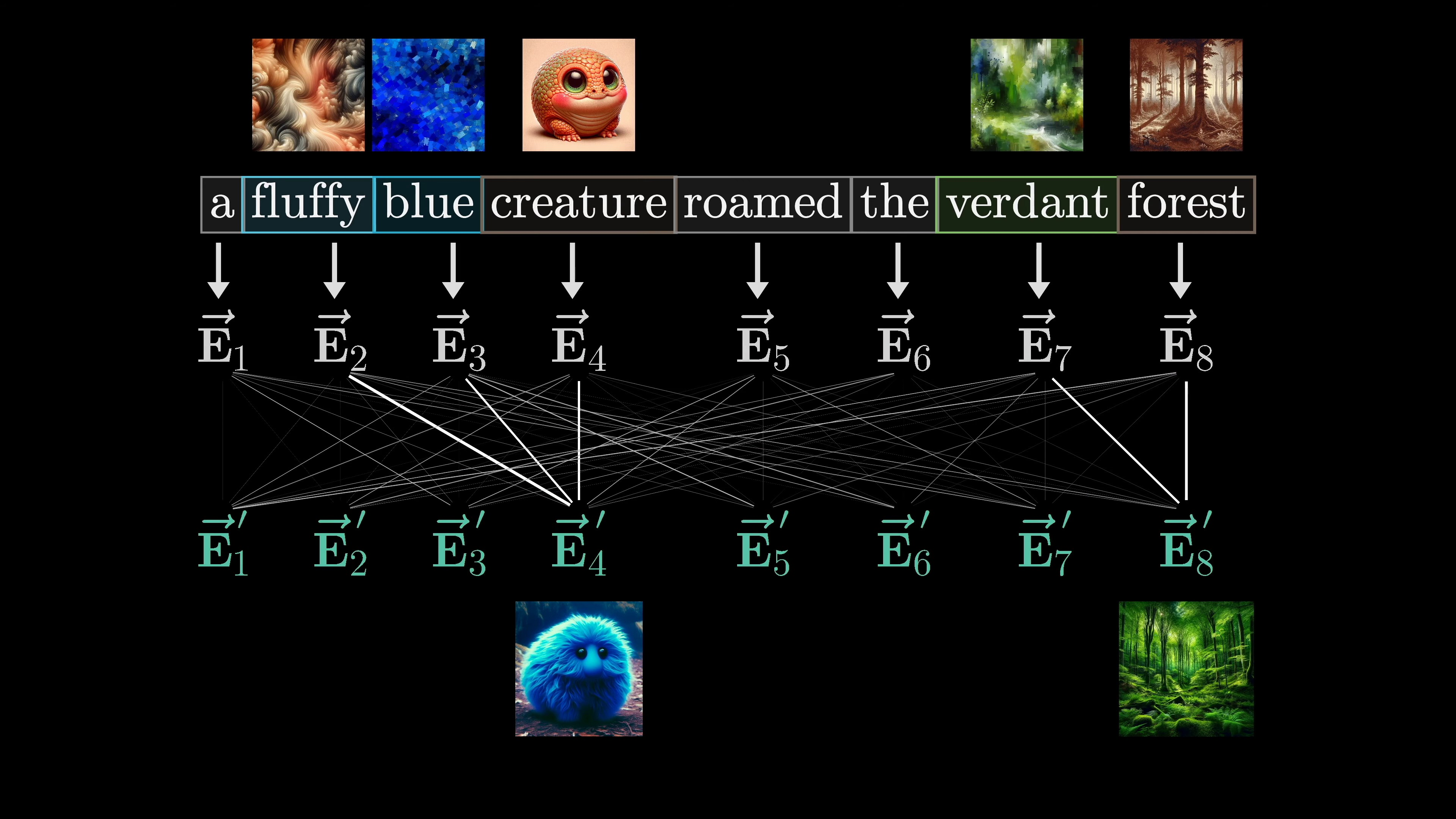
In order for the model to accurately predict the next word, the final vector in the sequence needs to be updated by all of the attention blocks to represent the relevant information from the full context window. Let's take a simpler example to understand this concept. Suppose the input is 'a fluffy blue creature roamed the verdant forest' and we only care about the adjectives adjusting the meanings of their corresponding nouns. Each word is initially embedded as a high-dimensional vector that encodes its meaning and position.

The Attention Block | 0:04:00-0:09:00
https://youtu.be/eMlx5fFNoYc?t=240
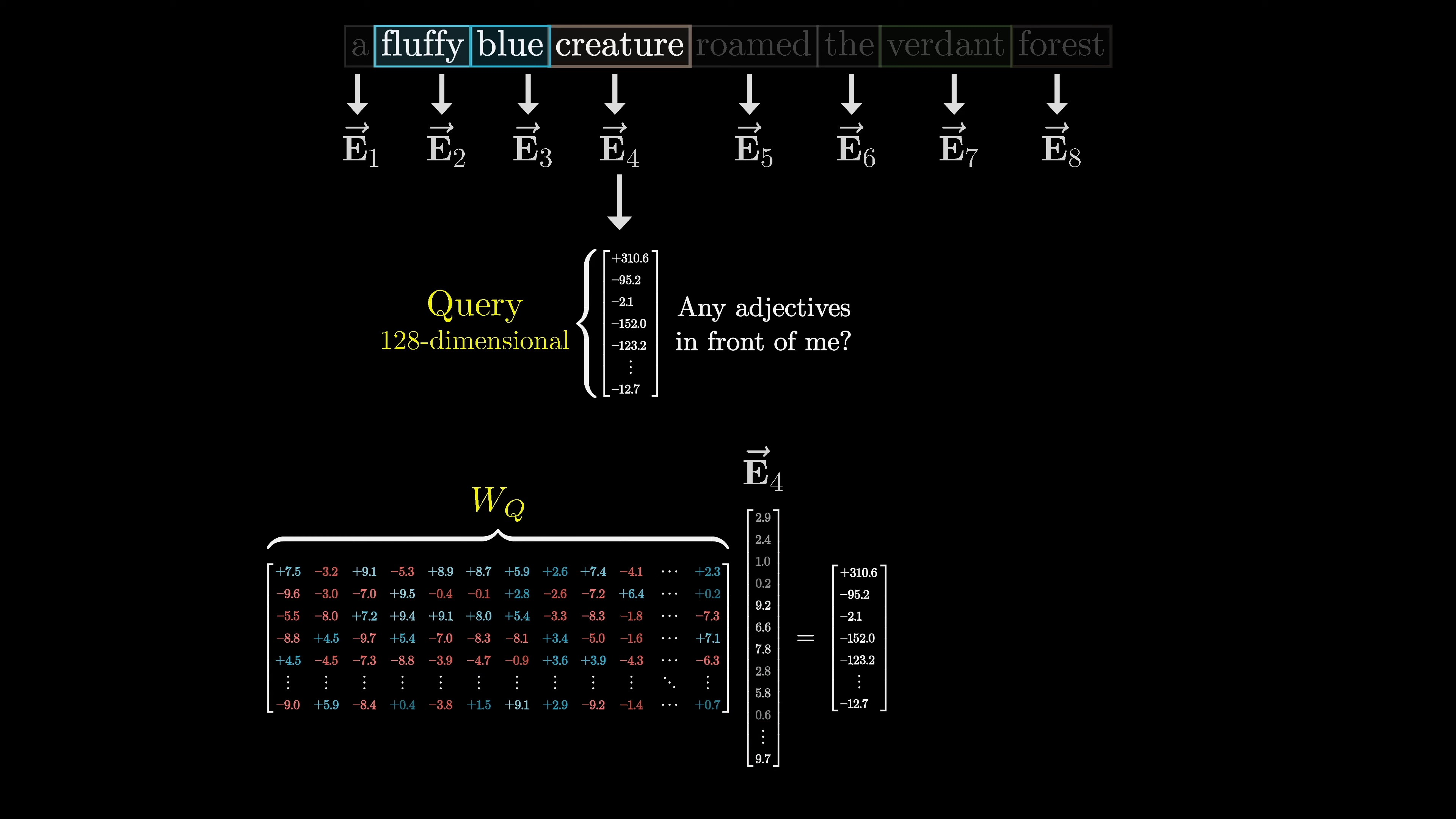
In deep learning, word embeddings are used to represent words and their positions in a context. The goal is to refine these embeddings by incorporating meaning from other words. This is achieved through matrix vector products, where tunable weights are learned based on data. For example, adjectives can update nouns by encoding the notion of looking for adjectives in preceding positions.
This is done by computing a query vector for each word, which is obtained by multiplying a query matrix with the embeddings.
Similarly, a key matrix is multiplied with the embeddings to obtain key vectors. The dot product between the keys and queries measures their alignment, indicating which embeddings attend to each other.
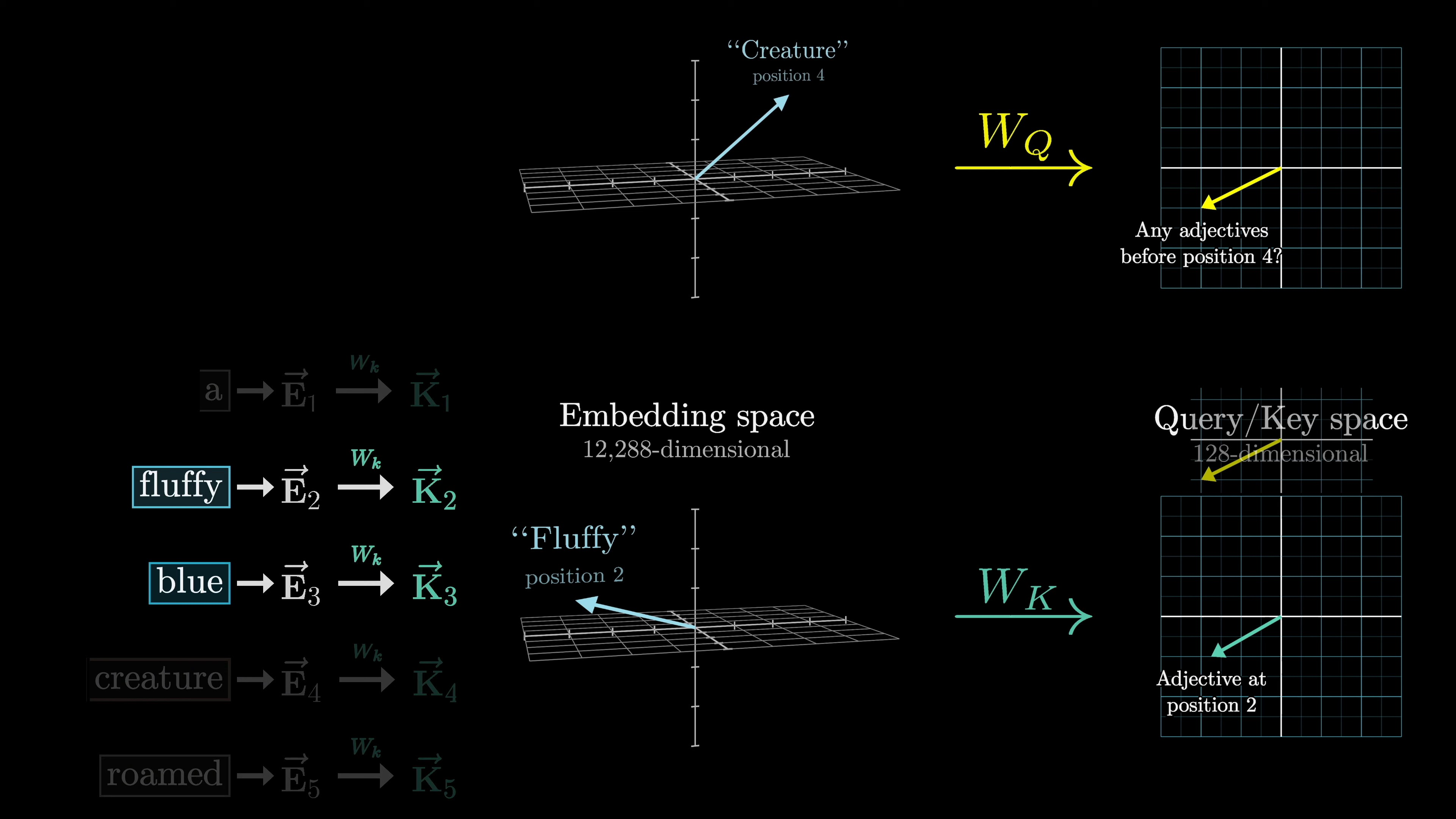
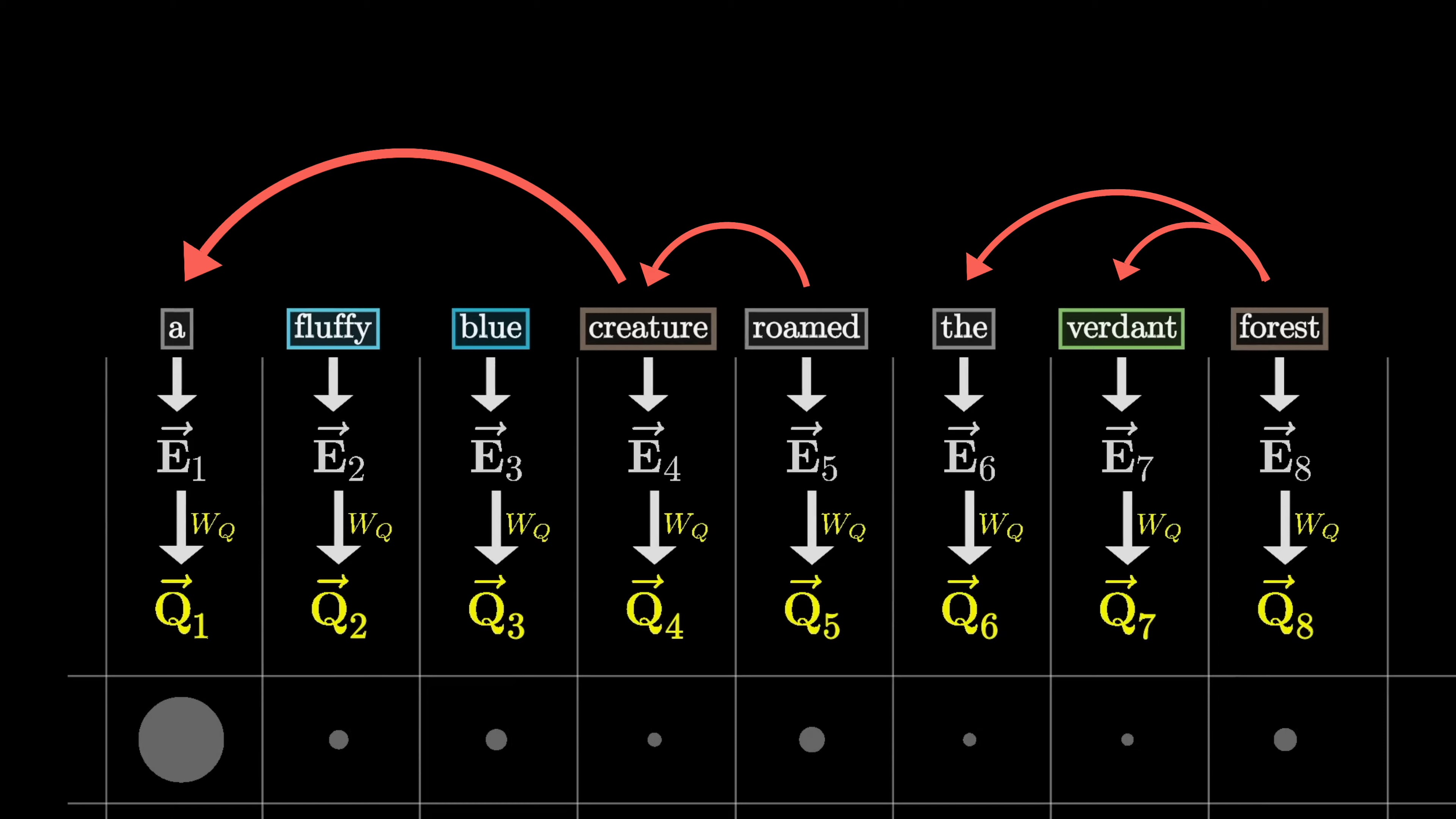
The embeddings of fluffy and blue would attend to the embedding of creature in our example. This process involves tuning a large number of parameters to minimize a cost function.
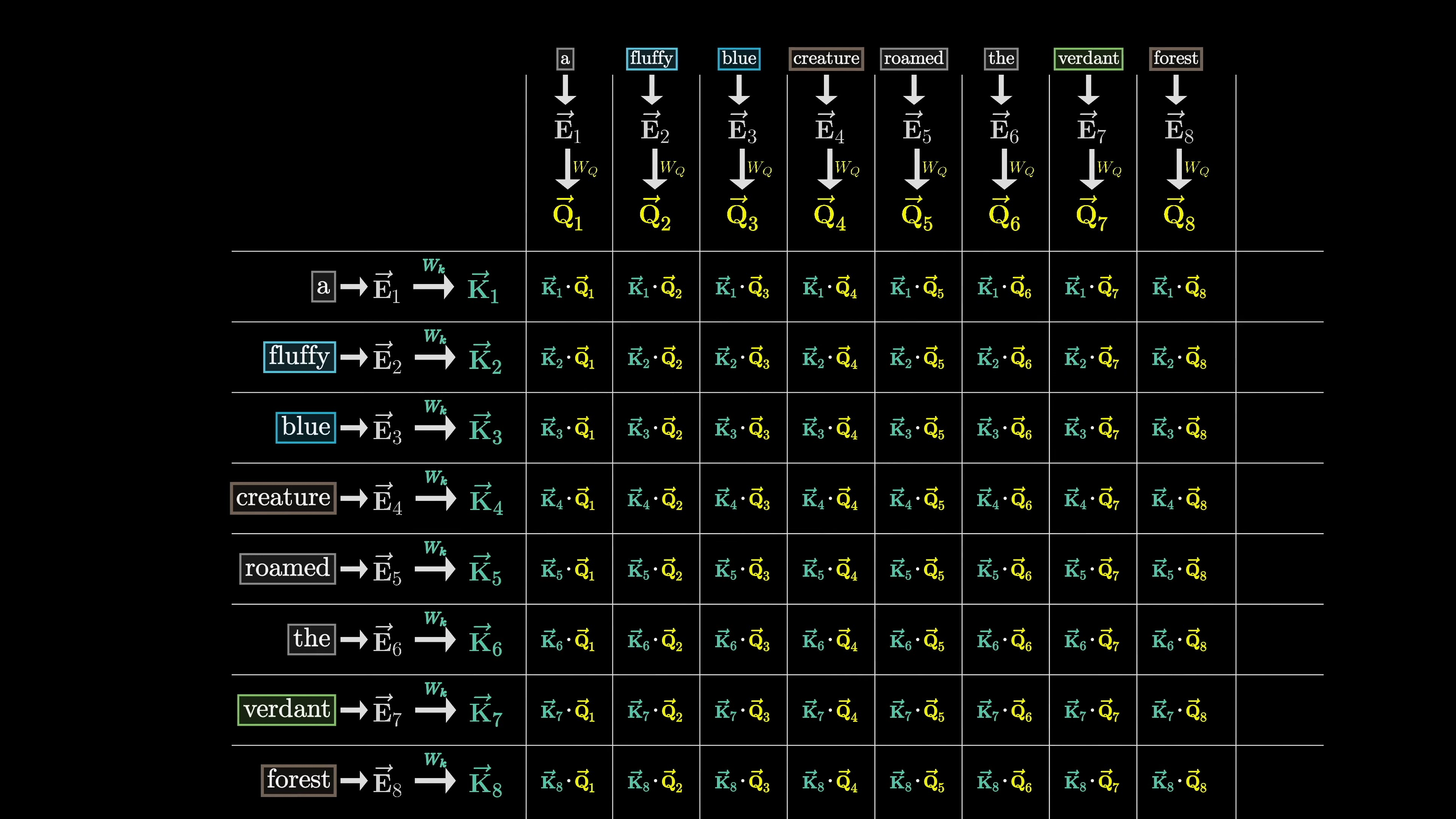
The magnitude of the relationships can also be seen.
The Attention Mechanism in Transformers | 0:09:00-0:20:20
https://youtu.be/eMlx5fFNoYc?t=540


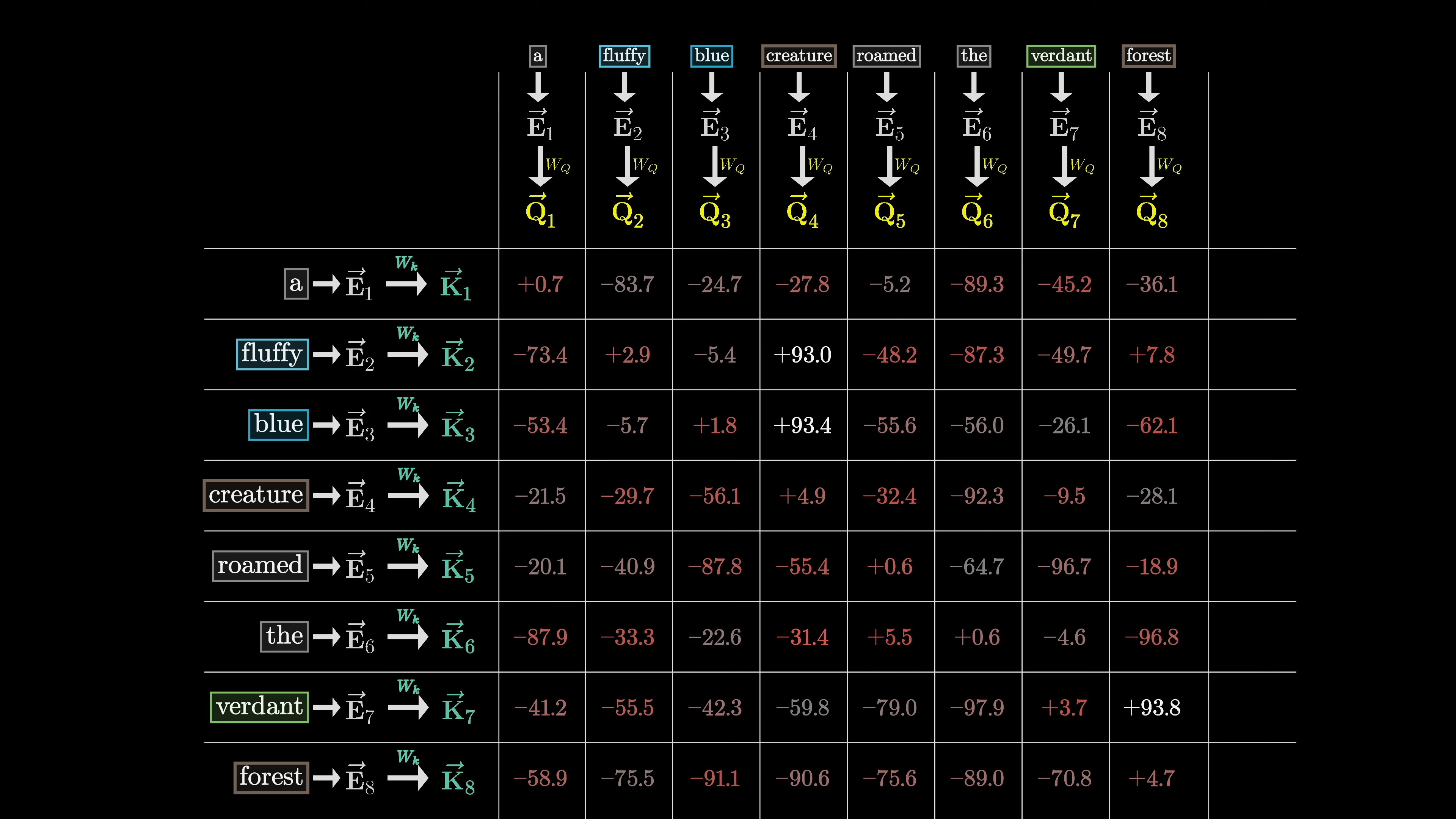
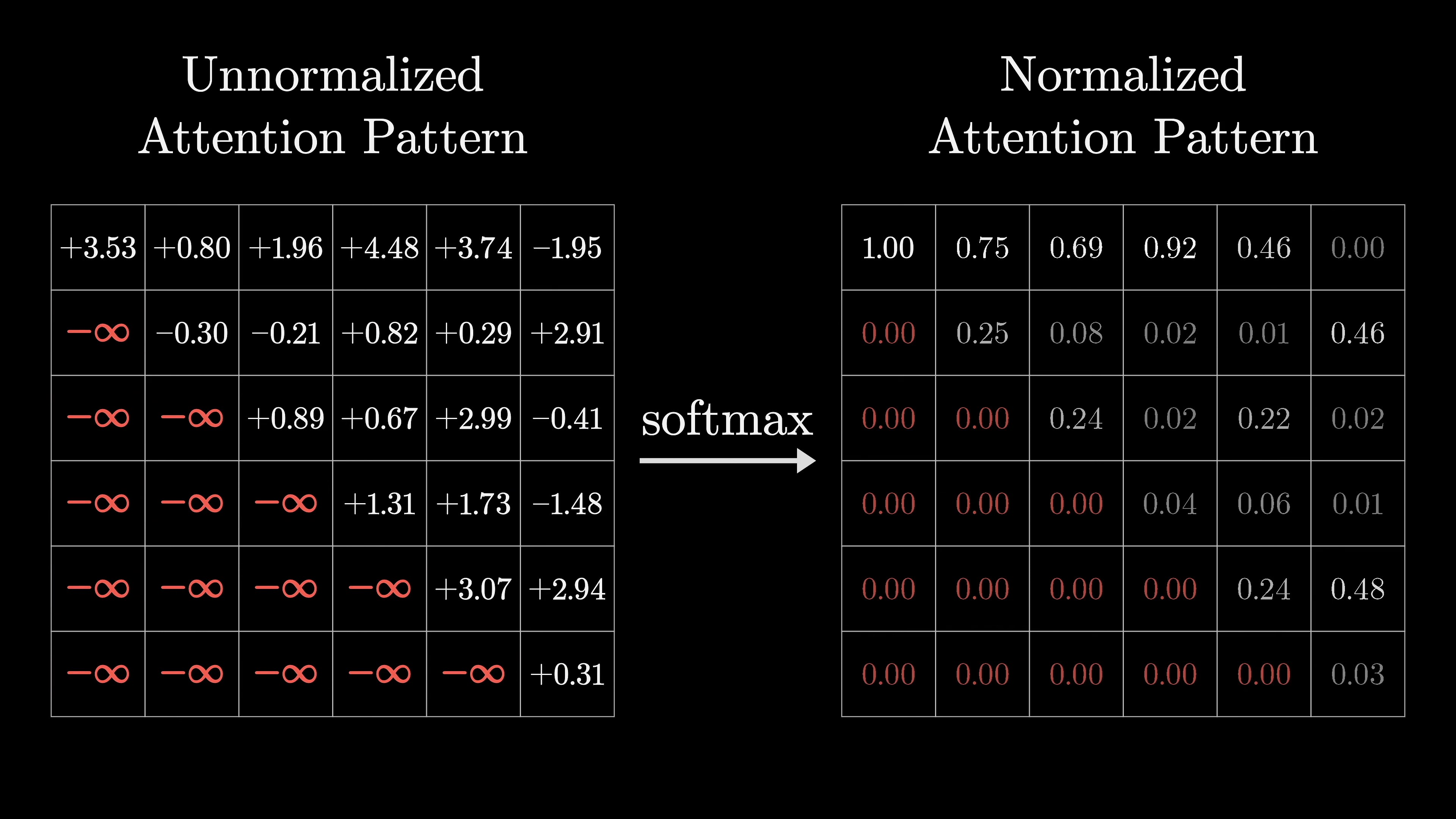
In the transformer model, we use a grid of values to represent the relevance between words. We normalize these values using softmax to create an attention pattern.

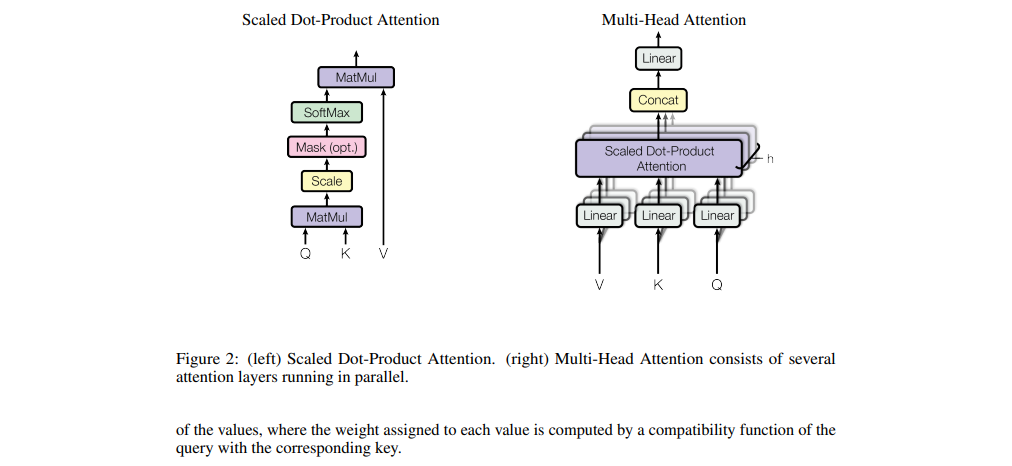
The variables Q and K represent the query and key vectors, and the numerator represents the dot products between keys and queries. We divide the values by the square root of the dimension for numerical stability. During training, the model predicts every possible next token for efficiency.

In order to prevent later words from influencing earlier words, we need to ensure that certain spots in the attention pattern are forced to be zero. Setting them equal to zero would disrupt the normalization of the columns, so we need to find another solution. A common approach to handle certain entries before applying softmax is to set them to negative infinity. This ensures that after applying softmax, those entries become zero while the columns remain normalized. The process of masking is used in GPT models to prevent later tokens from influencing earlier ones.
The size of the attention pattern is equal to the half of the square of the context size, which can be a bottleneck for large language models.
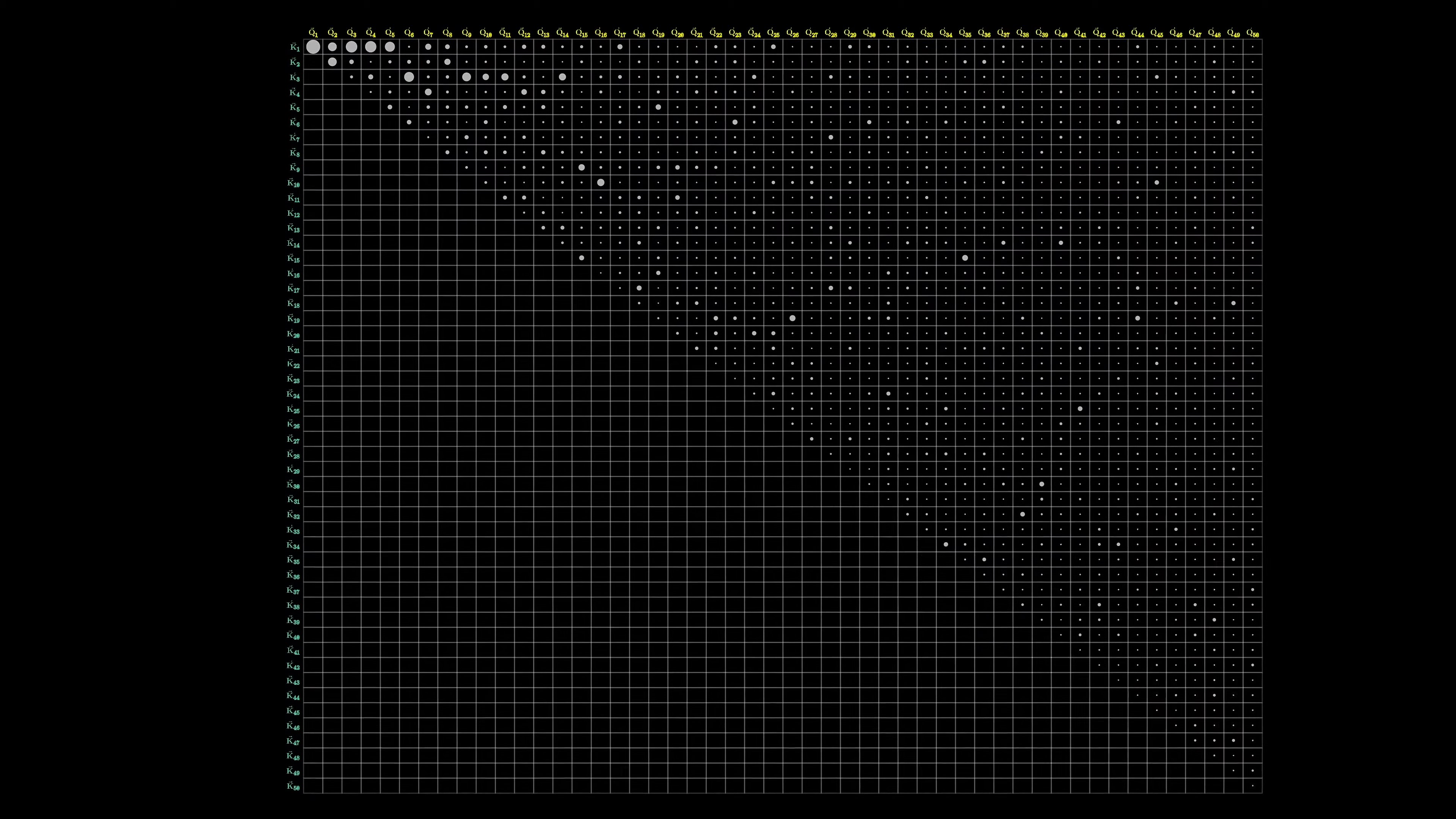
In recent years, there have been variations to the attention mechanism to make context more scalable. However, we will focus on the basics.
Computing this pattern allows the model to determine the relevance of words to each other. The embeddings need to be updated so that words can pass information to other relevant words. For instance, the embedding of 'fluffy' should cause a change in the embedding of 'creature' to encode a more specific representation of a fluffy creature in a 12,000 dimensional embedding space.
The most straightforward way to perform this task is by using a value matrix, which is multiplied by the embedding of the first word. This produces a value vector that is added to the embedding of the second word. The value vector exists in the same high-dimensional space as the embeddings.
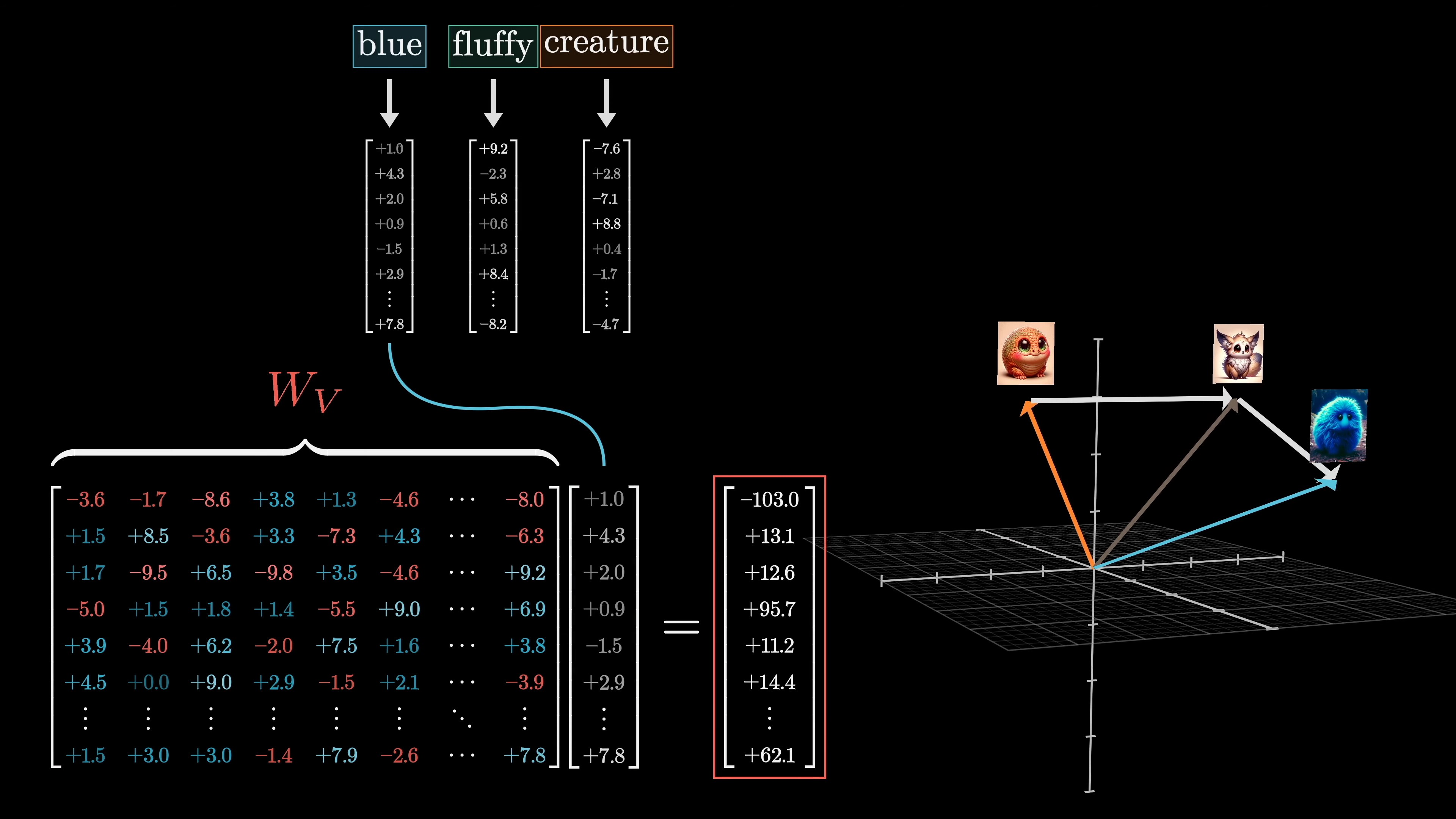
When multiplying a value matrix by the embedding of a word, it can be thought of as determining what should be added to the embedding of something else in order to reflect the relevance of that word in adjusting its meaning. In the diagram, the keys and queries are set aside.
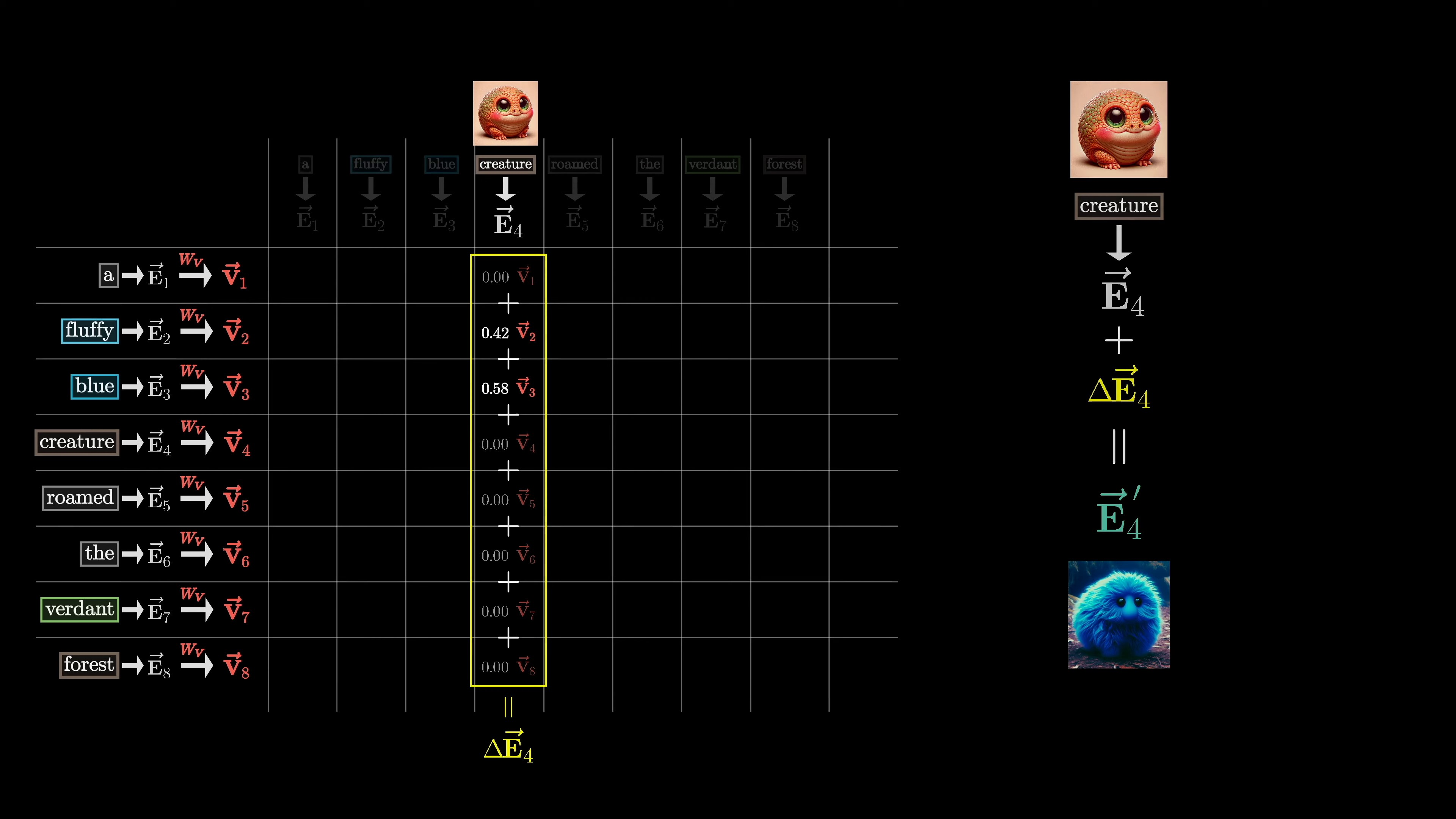
After computing the attention pattern, the value matrix is multiplied by each embedding to produce a sequence of value vectors. These value vectors are associated with the corresponding keys. Each value vector is multiplied by the corresponding weight in the attention pattern column. The resulting rescaled values are added together to produce a change (delta-e) that is added to the original embedding.

This process is repeated for all embeddings, resulting in a sequence of refined embeddings. This is a single head of attention. The process is parameterized by three matrices: key, query, and value, each filled with tunable parameters. In GPT-3, the key and query matrices have 12,288 columns and 128 rows, matching the embedding dimension.



To match the dimension of the smaller key-query space, the value map is factored into two smaller matrices: the value-down matrix and the value-up matrix. This allows for the same number of parameters to be devoted to the value map as the key and query. The overall value map is constrained to be a low-rank transformation.
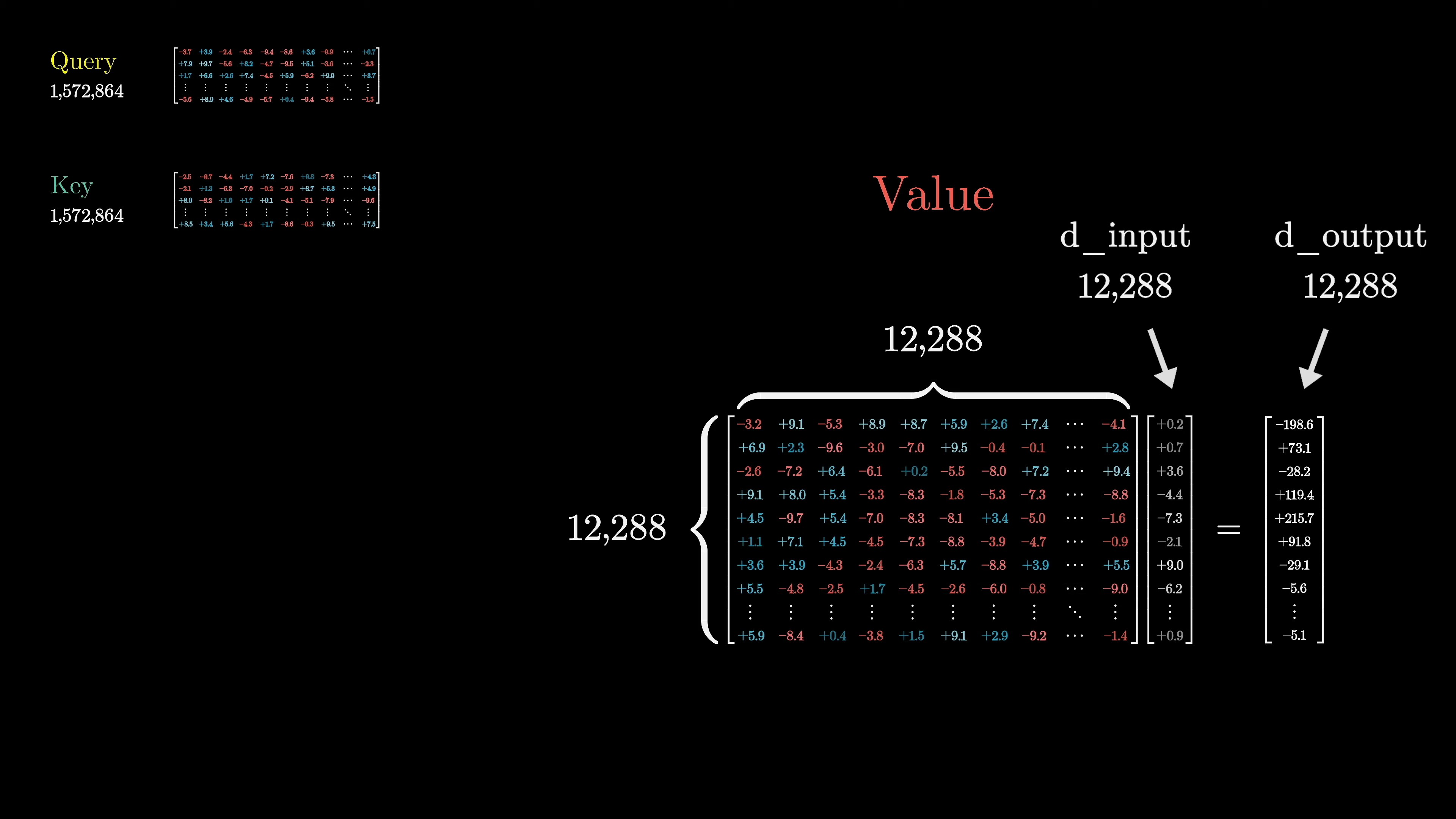
The value matrix above is decomposed as shown below.
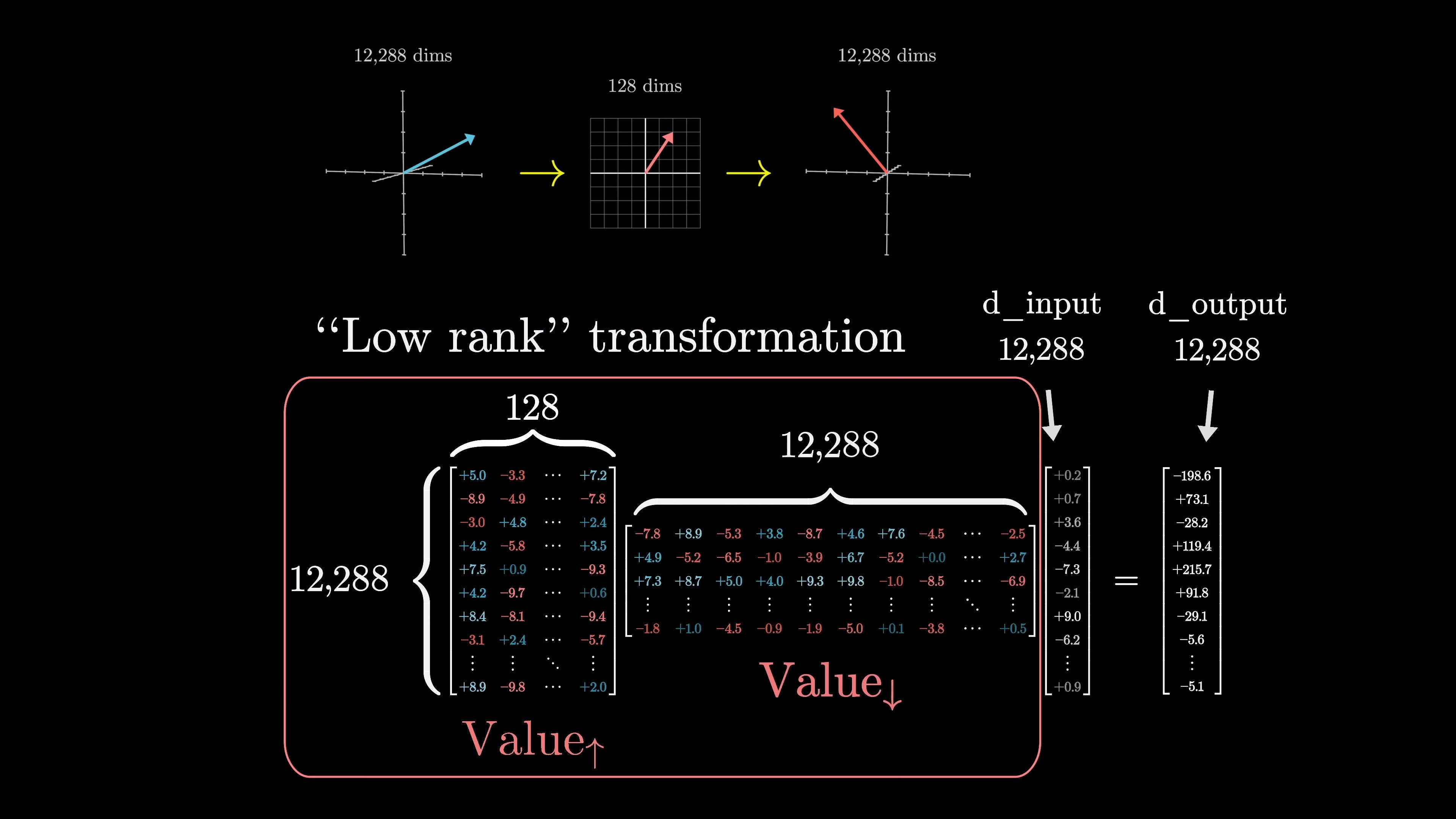
In total, there are about 6.3 million parameters for one attention head.
Self-attention heads are used in models that process the same type of data, while cross-attention heads are used in models that process different types of data. Cross-attention involves processing two distinct datasets, such as text in different languages for translation.
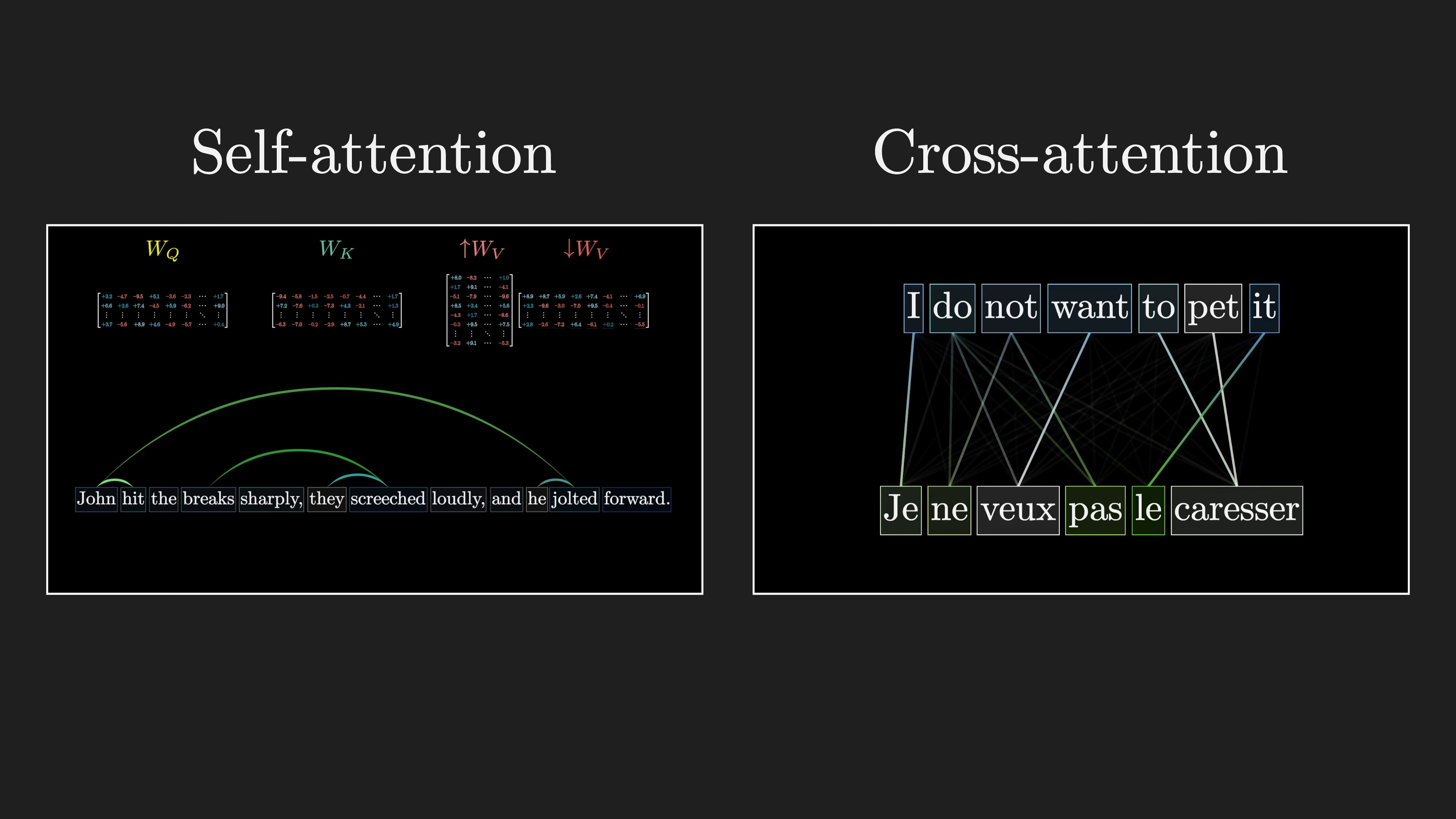
Self-attention does not require masking, while cross-attention may involve masking to determine word correspondences between languages.
The essence of attention is understanding how context influences the meaning of words. Context can update the meaning of a word in various ways, such as adjectives updating nouns or associations suggesting different references. Different types of contextual updating require different parameters in the attention mechanism. The behavior of these parameters is complex and determined by the model's goal of predicting the next token.
Multi-Headed Attention in GPT-3 | 0:20:20-10:10:10
https://youtu.be/eMlx5fFNoYc?t=1220

GPT-3 uses 96 attention heads in each block. Each head has its own key, query, and value maps. Each head produces a proposed change to be added to the embedding at each position. The proposed changes from all heads are summed together and added to the original embedding, resulting in refined embeddings. Running multiple heads in parallel allows the model to learn different ways that context changes meaning.
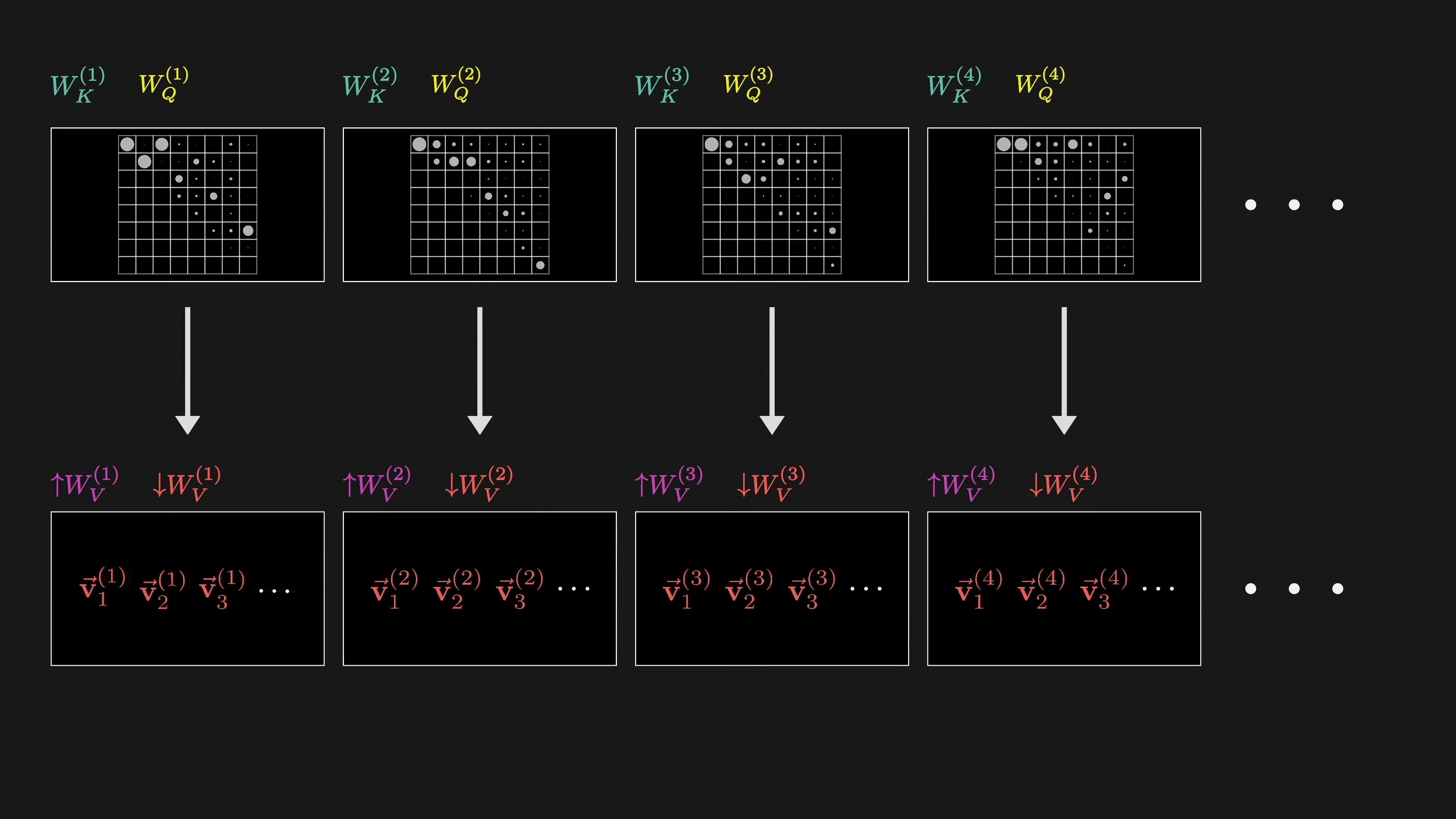
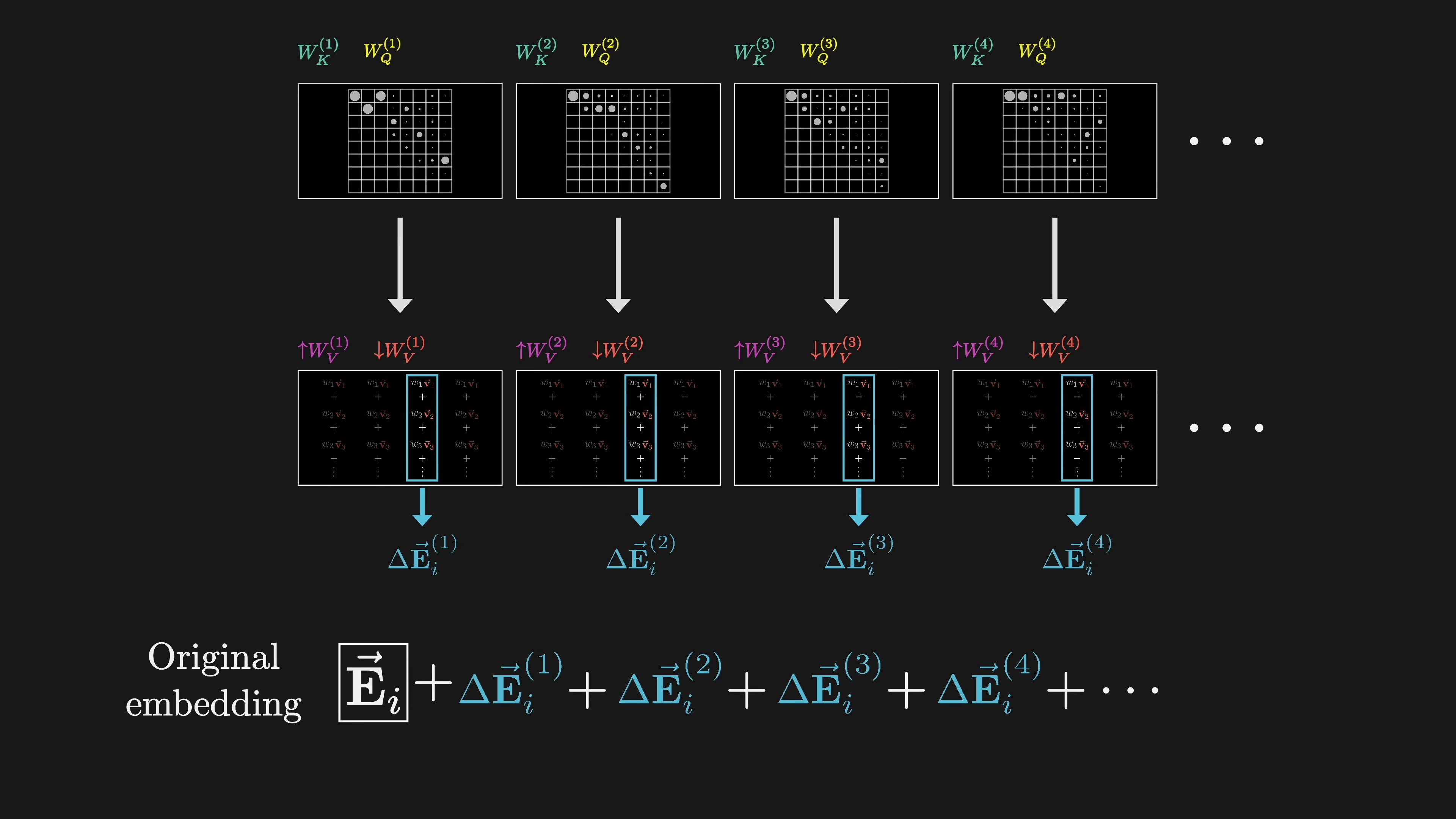
The running tally for parameter count is 96 heads, each with its own variation of four matrices, resulting in around 600 million parameters for each block of multi-headed attention. In transformers, the value map is split into two distinct matrices called the value down and value up matrices. While it is possible to implement these matrices inside each attention head, there is another way to do it.
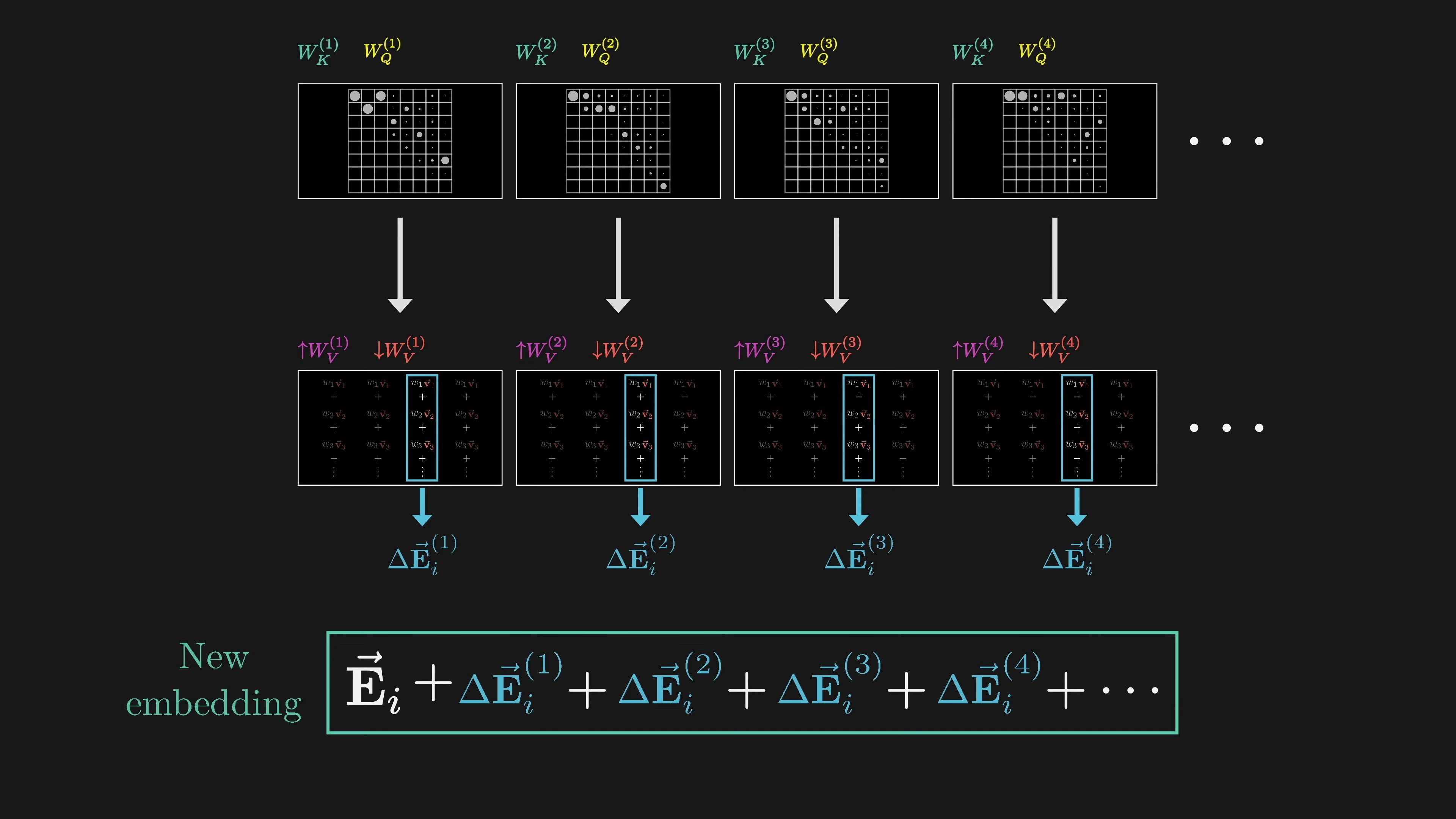
In practice, this implementation of multi-headed attention in transformers is different from how it is described in papers. The value matrices for each attention head are combined into one giant matrix called the output matrix.
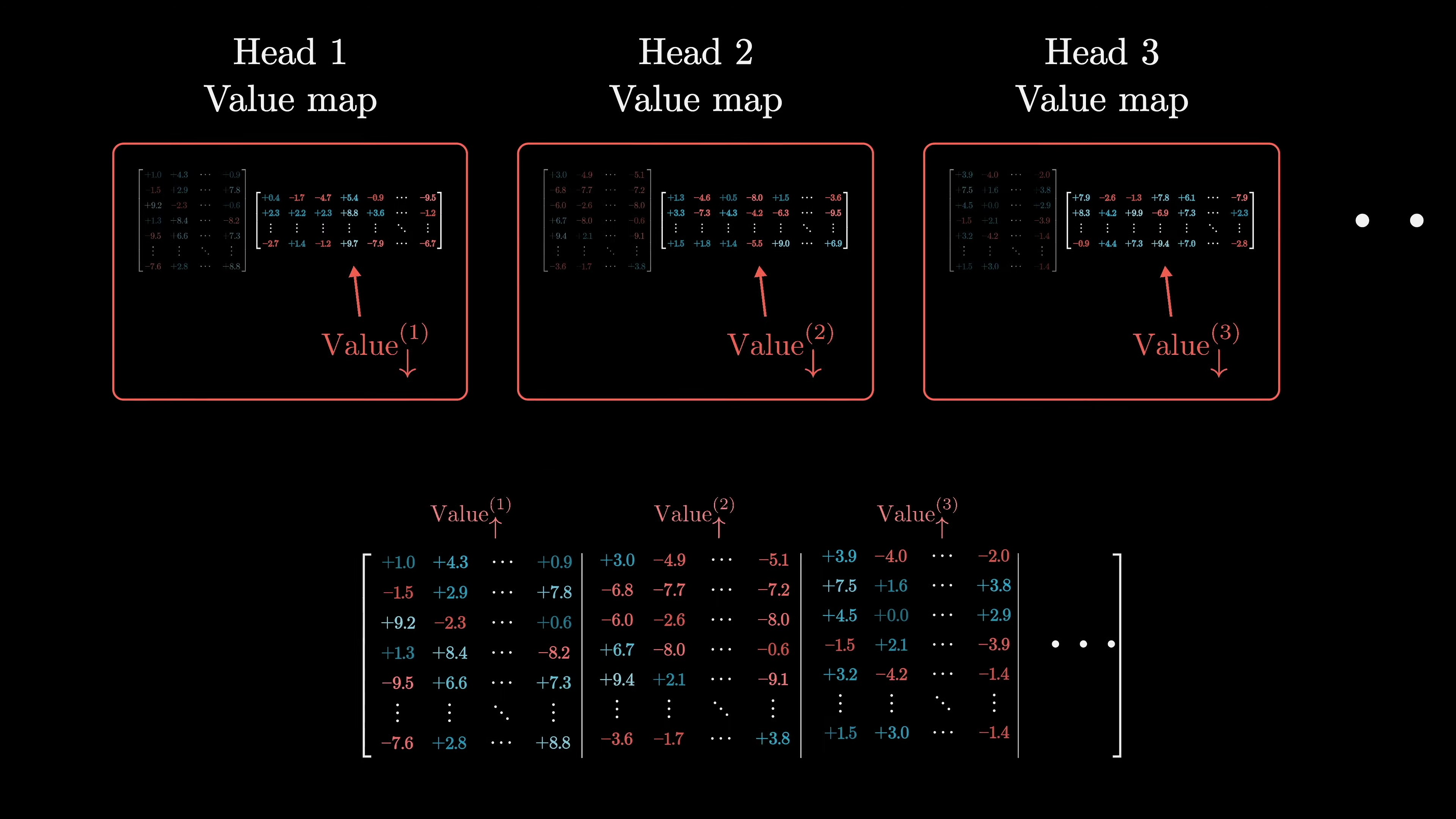
When people refer to the value matrix for a specific attention head, they are usually referring to the projection of values into a smaller space. Transformers consist of multiple attention blocks and multilayer perceptrons, allowing for the encoding of higher-level and more abstract ideas. GPT-3 includes 96 layers.
The attention mechanism in neural networks has a total of about 58 billion distinct parameters, which is about a third of the total 175 billion parameters in the network. While attention gets a lot of attention, the majority of parameters come from the blocks between the attention steps.
The success of the attention mechanism is attributed to its parallelizability, allowing for a large number of computations to be run quickly using GPUs. Scale alone has shown to improve model performance, making parallelizable architectures advantageous.
