The advertisements on this site are selected by me, and represent content that I believe is high quality or interesting. Purchasing content from these links helps me get paid as a content creator.

LLaMA Pro: Progressive LLaMA with Block Expansion (Paper Explained) - Yannic Kilcher

Yannic Kilcher Summary

Introduction of LLAMA Pro: Enhancing LLAMA 7b with Block Expansion | 0:00:00-0:09:00
Acquiring New Skills and Post Pre-Training Method for LLMs | 0:03:40-0:10:00
Challenges in Parameter Tuning and Knowledge Retention in LoRa Technology | 0:10:00-0:15:40
Residual Connection Zero Output Strategy | 0:15:40-10:10:10

Introduction of LLAMA Pro: Enhancing LLAMA 7b with Block Expansion | 0:00:00 - 0:09:00

https://youtu.be/hW3OVWfndLw?t=0

The paper introduces LLAMA Pro, a progressive LLAMA model with block expansion. It enhances a LLAMA 7b large language model by adding additional layers to it to teach it new information while preventing it from forgetting previously learned information. This approach allows for continual learning without the issue of catastrophic forgetting. The model is designed to retain existing knowledge while incorporating new knowledge. In the example provided, a base model called llama 2 is expanded to llama pro and then fine-tuned to become the chat model llama chat.

There is even an A Llama 2 instruct, right?

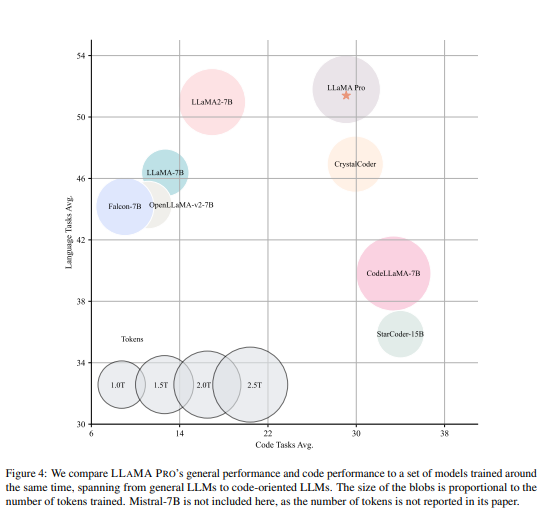
Another model also gets instruction tuned to become the instruct model. They compare the two resulting models right here, one being just a regular process and one being the result of this block expansion route adding in new data. So once you do that, the original llama, as you can see, is pretty good in some tasks but then falls short on other tasks. Now what are these tasks? These tasks are things like coding, these tasks are math and coding benchmarks.

There are limitations of a coding model like Code Llama in language understanding benchmarks and abstract reasoning. The data inputted into models reflects their capabilities. By adding data containing code and math, the model can improve in these areas without losing its original strengths. The process involves adding layers, freezing existing ones, and fine-tuning the new layers. The goal is to enhance the model's performance in specific tasks while maintaining its proficiency in others.

Acquiring New Skills and Post Pre-Training Method for LLMs | 0:03:40 - 0:10:00

https://youtu.be/hW3OVWfndLw?t=220

They say, "Humans generally acquire new skills without compromising old ones." I don't necessarily believe that's true. For instance, if you played an instrument when you were younger and then stopped playing it for a long period, you have to relearn it. You no longer remember the songs, and your muscle memory isn't as sharp. But I'll concede that machine learning models often exhibit forgetfulness.

Consider the proposal of a new post pre-training method for Large Language Models (LLMs). What exactly is post pre-training? Pre-training generally refers to the initial training of the LLM, which is conducted on a vast corpus. Afterwards, there's fine-tuning via instruction. This post pre-training sits between the pre-training and the instruction tuning, hence the term "post pre-training."

The claim is that this method can efficiently and effectively enhance the model's knowledge without the model suffering from catastrophic forgetting. Experiments were conducted on a corpus of code and maths, resulting in a new model based on LLM that excels in general tasks, programming, and mathematics.

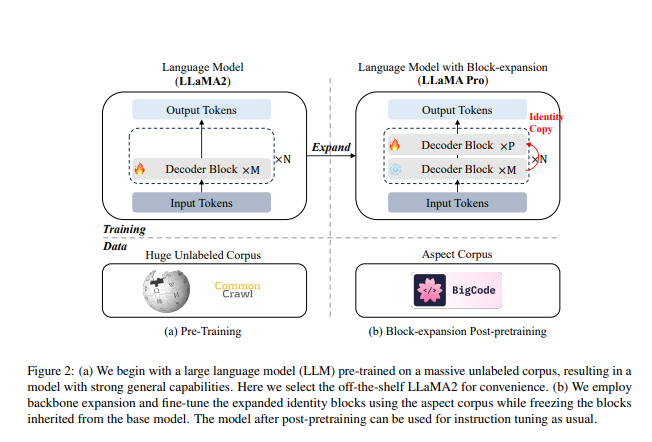
To illustrate the architecture of LLM, consider a model with an input layer that offers token embeddings for the input, and an output later. The designation as tokens is subject to dispute; they might be more accurately called embeddings or embedding weights. The input embedding is then passed through layers, or blocks, of transformative elements containing attention mechanisms, normalization, feed-forward layers, and so on. The present trend in machine learning, circa 2023-2024, is largely: repeat this process numerous times and input the data.

So, given this architecture, the proposal is to duplicate these blocks and focus training on the copies. This could mean selecting specific layers, duplicating them, and inserting them at the desired location.

Copying a layer in a neural network might seem as though it would substantially alter the output signal by introducing duplicate computations. However, the existence of residual connections in neural networks aids in minimizing this issue. Residual connections involve adding the input signal to the output signal of a layer, ensuring smooth data and gradient flow. If a layer is initialized such that its output is zero, the overall network output remains unaltered. This is because the signal from the preceding layer branches into two: one follows the identity function, while the other flows through the block. When the output of the block is set to zero, only the identity function progresses in the network.

So, if you can design your new layer in such a way that its initial output is zero, then at least immediately after copying, you have the same network - that's something we can all agree on. Where it becomes a bit controversial, I believe, is when they suggest that during training, we should only train the newly added layers. So, we're only going to train these added layers and everything else will have frozen parameters. We simply forward propagate, backpropagate to these new layers, and modify the new layers, which will inevitably cease their zero outputs. Consequently, this block becomes active in these new tasks and starts contributing to the signal.

Challenges in Parameter Tuning and Knowledge Retention in LoRa Technology | 0:10:00 - 0:15:40

https://youtu.be/hW3OVWfndLw?t=600

The process of adding parameters and fine-tuning them, particularly in the context of LoRa technology. However, I am skeptical about claims that a system can retain old knowledge while incorporating new knowledge. I doubt the system's ability to differentiate between old and new data, i.e., that every signal is processed through a layer and alters the output. I question whether the training process includes a mix of old and new data to ensure accuracy, which I believe is not the case based on my observations.

LoRA: Low-Rank Adaptation of Large Language Models

They only train with in-domain data, so the network primarily sees this new data. While it cannot adapt the old parameters, rendering it technically incapable of forgetting anything, it can configure new parameters such that the signal from the old parameters is distorted. There's no loss in retaining that data and no signal directing it to silence the new layers because they belong to the old domain. I believe this approach works as long as the new data significantly overlaps with the old data. For instance, I anticipate that there will be plenty of code already present in the math pre-training data of LLAMA, and that these overlaps could be sufficient. However, I would be surprised if this served as a universal strategy for more drastic domain adaptations without incorporating some of the old data. In any case, this is essentially what they do. They duplicate every nth layer, ensuring it initially outputs zero. They then change the necessary weights to make it output zero before training solely with those weights active and keeping the rest frozen. That's the gist of it.

There are limitations to improving pre-trained language models (LLM) due to the need for significant computational resources and vast amounts of data. They introduce Llama2B, which involves pre-training expanded blocks on 80 billion tokens using open source code and math data for 2830 GPU hours. They mention using 16 NVIDIA H800 GPUs for seven days. There are substantial data and compute requirements to address the challenge of catastrophic forgetting and decline in model abilities in other approaches.

Residual Connection Zero Output Strategy | 0:15:40 -

https://youtu.be/hW3OVWfndLw?t=940

There are differences between original llama blocks and those created after identity copying, i.e., the nature of the process is complex and large-scale. The left-hand side represents a layer in the original network, while the right-hand side represents a copied layer.

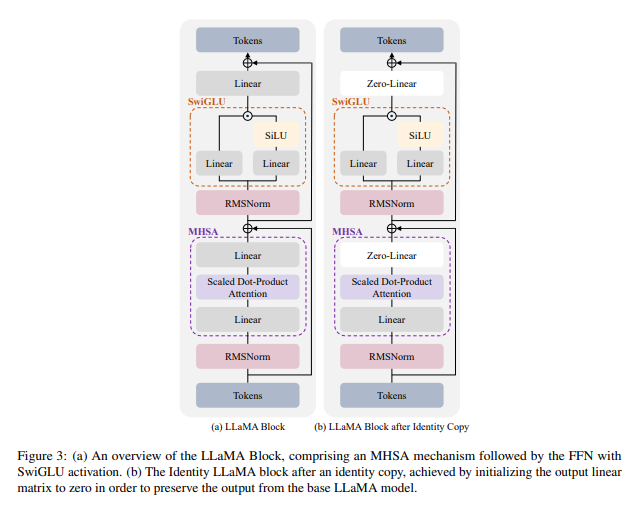
Modifications to the copied layer are made by changing certain points to zero. This ensures that the output is identical. Thus, residual connections are demonstrated here, here, and here. If we can ensure that this output is zero, everything is good. Since it's a feed-forward layer, the most effective way to achieve zero output is by making the weight matrix zero. This procedure multiplies everything by zero, resulting in zero output. Then, we see this object, another residual connection with a linear operation preceding it. Setting it to zero also guarantees that the entire construction is merely the residual connection at the commencement. Obviously, all the weights contained herein will be updated during training.

It would be fascinating to trace what happens if only these linear elements are updated. Diving a bit into the mathematics, apart from this operation, there is an output weight matrix. The results of the attention are placed in here and then multiplied by this output weight matrix. This presents an excellent opportunity for manipulation simply by setting it to zero. Equally, the second component, an element of the feed-forward network, incorporates some non-linearity but ultimately it's also multiplied by an output weight matrix, another good point to reduce to zero. This ensures that all outputs are set to zero, making the entire thing identical.

Is this approach beneficial? It's not entirely clear. Preserving the parameters in the rest of the layer is undoubtedly an ingenious move as there are presumably some reusable primitives contained within. However, copying this information may not be desirable. In my perspective, this technique could potentially be more like a few low-rank adapters designed together and then passed through these layers, rather than duplicating the entire construct. If there's fine-tuning once it's already trained, a slight adjustment can be made.

There is an impact to the different parameters in the model, and I question whether zero-initialized linear layers will regress to the old layer or find a new forward propagation. It is important to consider the scaling in the forward signal to avoid instability. There may be smarter ways to achieve desired outputs without zero initialization. I ponder the challenge of achieving zero output with residual connections and question the necessity of introducing new layers.

I find it amusing that only every fourth block is expanded in the model architecture. However, this paper mentions incorporating an identity block after each block to maintain the same output for expansion and that other paper had an idea of initializing scaling parameters to zero in norm modules for the construction of the identity block, but explains why this approach may not be effective for LLAMA. I looked up this other paper on stage training for transformer language models, which takes a general approach to training models successively. The new paper doubles the number of layers using a depth operator, adding an identity layer after each layer. I speculate that the new paper may have been inspired by the previous paper but required a different approach for LLAMA. The adaptation of ideas is seen as a common practice in research.

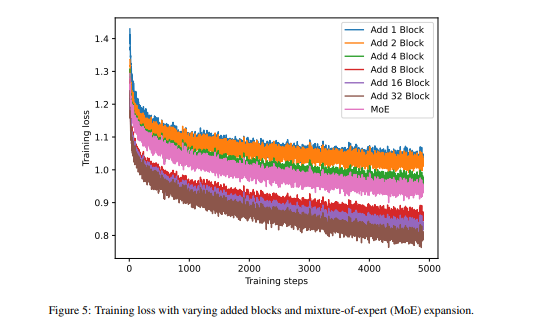
There are a few more comments that find potential errors in the paper after this.

LLaMA Pro: Progressive LLaMA with Block Expansion (Paper Explained)

Affiliate Marketing