The advertisements on this site are selected by me, and represent content that I believe is high quality or interesting. Purchasing content from these links helps me get paid as a content creator.

Promptbreeder: Self-Referential Self-Improvement Via Prompt Evolution (Paper Explained) - Yannic Kilcher

Yannic Kilcher Summary

Prompt Breeder: Self-Referential Self-Improvement via Prompt Evolution | 0:00:00-0:01:20
Limitations of Large Language Models | 0:01:20-0:03:20
A General Purpose Self-Referential, Self-Improvement Mechanism for Prompt Evolution and Adaptation | 0:03:20-0:06:40
Challenges in Automated Prompt Engineering | 0:06:40-0:11:00
Types of Prompts: Thinking Styles, Problem Description, Mutation Prompts | 0:11:00-0:15:40
Approach to Task Evaluation and Evolution in Language Models | 0:15:40-0:21:00
Population-based Algorithms and Mutation Operators | 0:21:00-0:28:40
Conditioning on Parents for Task Prompt Generation | 0:28:40-0:36:20
PromptBreeder Strategy | 0:36:20-

Prompt Breeder: Self-Referential Self-Improvement via Prompt Evolution | 0:00:00-0:01:20

https://youtu.be/tkX0EfNl4Fc?t=0

Hello there! Today, we're going to delve into "Prompt Breeder: Self-Referential Self-Improvement via Prompt Evolution". This is a paper by Google DeepMind, the new consortium that amalgamates Google Brain and DeepMind. It promises to be an intriguing exploration.

The fundamental principle behind this paper is that instead of manually creating your own prompts for large language models to perform a specific task, you utilize a system that inherently evolves prompts. Essentially, you provide it with a task description, and it generates its own prompts to enable a large language model to tackle the task. Intriguingly, the generation of these prompts is carried out by large language models themselves, utilizing an evolutionary algorithm.

If you're familiar with evolutionary algorithms, you'll know they depend on mutation and fitness evaluation. In this specific paper, even the mutation part is conducted by large language models. As such, this contributes to its self-referential and self-improving nature as it enhances its own method of generating improved prompts. We'll delve deeper into this. It all becomes quite complex,

Limitations of Large Language Models | 0:01:20-0:03:20

https://youtu.be/tkX0EfNl4Fc?t=80

The use of a large language model to handle various tasks and the results may seem promising, I believe the approach does not completely solve the problem but rather shifts it to a different domain. It might require further examination of the results to reveal that the problem persists despite the use of the language model.

Strategies like 'chain of thought' prompting can significantly enhance the reasoning abilities of large language models. By breaking down tasks into smaller steps and prompting the model to think step by step, the accuracy of the model's answers can be greatly improved.

Techniques such as 'chain of thought', 'tree of thought', and 'step by step' prompting have been developed to help language models perform better by explicitly guiding them through problem-solving processes.

A General Purpose Self-Referential, Self-Improvement Mechanism for Prompt Evolution and Adaptation | 0:03:20-0:06:40

https://youtu.be/tkX0EfNl4Fc?t=200

"PromptBreeder" is a paper that introduces a general-purpose self-referential self-improvement mechanism for evolving and adapting prompts within a given domain. This mechanism eliminates the manual process of constructing prompt strategies by automatically generating suitable prompts for tasks such as solving math problems. It offsets the need for individuals to think sequentially and manually write formulas and results, making the process more efficient and effective.

The mechanism employs an evolutionary algorithm to evolve task prompts. A key point in this paper is that the Prompt Breeder is not only improving task prompts, but it is also enhancing the mutation prompts that aid in bettering these task prompts; this is the self-referential aspect. Reasserted here is that prompting is central to the downstream performance of foundation models. If one agrees with the concept of foundation models, you might perceive that it is being used a bit inaccurately here because prompting specifically pertains to language models and technically doesn't relate to foundation models as such. While some models that I can prompt could be classified as foundation models, others definitely would not align with the vague original terminology surrounding that term. Moreover, there exist foundation models that currently cannot be prompted according to the unclear definition of a foundation model. This point seems more akin to a marketing department's parroting than a serious research organization.

Regardless, that's just a minor gripe of mine. But, in any case, the importance of prompting is acknowledged. However, prompt strategies are primarily constructed manually, leading people to ask: Can this prompting engineering be automated? There have already been some explorations in this direction. The Automatic Prompt Engineer, or APE for short, is an attempt in this regard. The process involves generating an initial distribution of prompts using another prompt that discerns the problem from several input-output examples derived from the dataset. In this case, a portion of the dataset acts as a training set, providing demonstrations of how the process is correctly done. From these examples, the aim is to infer a prompt that, much like classical machine learning,

Challenges in Automated Prompt Engineering | 0:06:40-0:11:00

https://youtu.be/tkX0EfNl4Fc?t=400

In automated prompt engineering, examples are utilized to train a model to generate the correct prompts. This resembles how data is used in training a regression model. Despite efforts in this field, the results have indicated diminishing returns.

As they relentlessly strive to refine the prompt, they hit a ceiling relatively quickly. The authors propose a solution to this problem of diminishing returns via a diversity-maintaining evolutionary algorithm for self-referential self-improvement prompts of LLMs. They argue that previous automated prompt engineering efforts didn't yield significant results because they lacked the maintenance of diversity during the improvement of their prompts. After achieving initial progress, if the focus remains in that direction, a limit is inevitably reached. However, maintaining diversity, a well-known technique in many exploratory black box optimizers, can prevent hitting this limit. If you're interested in learning more about these concepts, there are comprehensive studies on open-ended learning and goal-free learning among others, originally authored by Kenneth Stanley and his colleagues.

This paper touches on the concept of maintaining diversity of solutions. The advantage of retaining diversity is that when one reaches a point where further improvement is not possible, ideas may be borrowed from diverse sources, combined, and applied to new solutions, avoiding stagnation. The results demonstrate that, on multiple datasets in both zero-shot and few-shot learning, they significantly surpass other methods. It should be noted that the figures represented are not the original numbers if compared to other papers. Instead, they have been subdivided into training and testing samples.

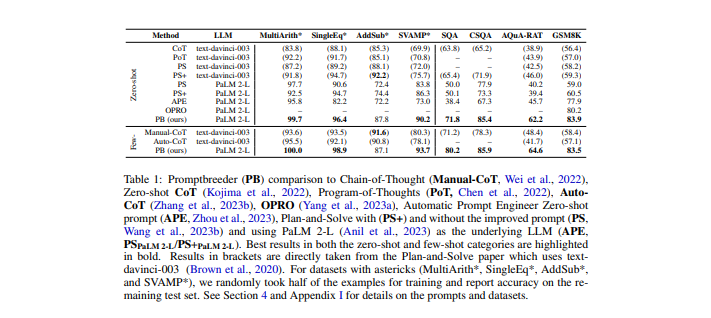
In the realm of large language models (LLMs), zero-shot techniques can sometimes solve tasks, as stated in the initial paper on LLM's multi-task zero-shot learning. The GPT-2 or GPT-3 paper discusses this, but we have returned to the scenario where actual training data are used. These prompts improvement systems operate by consuming the training data, which are records of successful task executions.

Types of Prompts: Thinking Styles, Problem Description, Mutation Prompts | 0:11:00-0:15:40

https://youtu.be/tkX0EfNl4Fc?t=660

So, how does Prompt Breeder function? They begin with an initial set or population of task prompts and mutation prompts. Actually, they have three kinds of prompts followed by some constant prompts. Then, there are these various thinking styles. It's somewhat perplexing to me why they're included. Essentially, I can comprehend that at some stage this concept probably wasn't as effective as anticipated. So, they proceeded to introduce different thinking styles to enhance diversity. These thinking styles, however, are merely a list of strategies. For instance, one strategy might be to approach a problem step by step, while another could involve breaking the problem down into smaller parts. These are not specific to any particular problem but are more general heuristics to try to think outside the box or reformulate concepts.

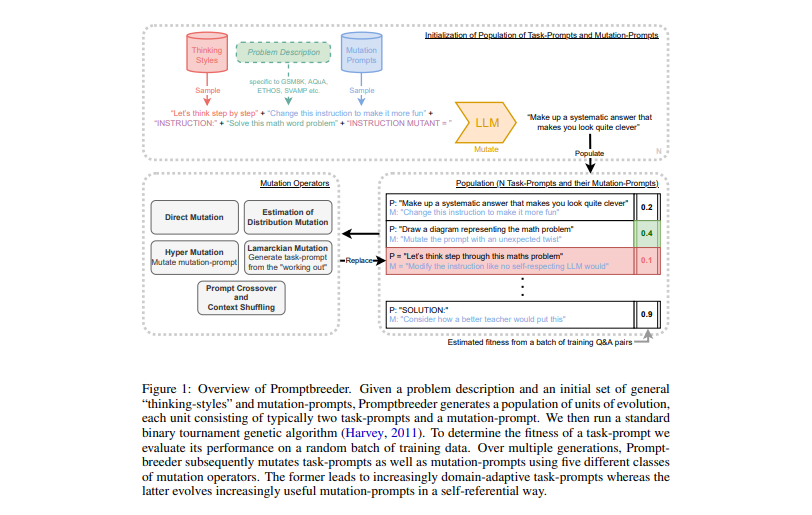
Undeniably, though they may seem out of place, these thinking styles were likely implemented to improve the system's performance. The problem description is explicit to the task you want to solve, such as solving a math problem, with the answer given as a precise number, for instance. Then, of course, there are the so-called mutation prompts.

Mutation prompts unfold the idea of manipulating one task prompt, denoted here as 'P,' i.e., to make it more enjoyable by integrating it with a mutation prompt. This process involves an instruction such as 'Change this instruction to make it more fun,' coaxing the language model to generate a variation of the original prompt. Over time, both the original task prompts and mutation prompts are expected to evolve, thereby improving. This process necessitates iteratively modifying the original task and mutation prompts to enhance the generation of intriguing content.

In addition to regular prompts and mutation prompts, there's the initial problem description, a list of thinking styles, and some structured components, such as the meta-prompting process. However, that does not include the mutation operators, which we'll discuss later. To generate the initial population, the original problem description is taken along with an initial set of mutation prompts to create several variations.

One aspect that I found a bit confusing while reading the paper was their use of terms such as 'units of mutation' and 'unit of evolution.' A 'unit of evolution' is a mutation prompt, coupled with two additional prompts, P1 and P2, as far as I understand. The mutation prompt could be an instruction to reformulate, to make it more fun, better, or more concise. Then, P1 and P2 are specific prompts like 'solve this math problem.' However, the way they use these two prompts isn't exactly clear to me. Still, if we consider most tasks, this is probably how they are implemented.

Approach to Task Evaluation and Evolution in Language Models | 0:15:40-0:21:00

https://youtu.be/tkX0EfNl4Fc?t=940

When you're presented with a task, such as during evaluation time, you first approach it as 'problem one', where you outline the math question before engaging the Language Learning Model (LLM). You then allow the LLM to produce a potential solution. This could already be the correct response, but you also provide a second prompt to allow the LLM to produce an alternative. This second output is then checked for correctness. Often, you have the opportunity to instruct the LLM in problem-solving and to get it to present its solution in the correct format. A common approach is to initially instruct the LLM on how to solve the problem. The LLM will typically provide a response such as 'here is the solution', staffed with the desired solution. It has become common to put in the initial prompt to 'only provide the solution', to guide the output. This two-prompt method ensures the focus remains on providing both a solution and the correct format for the answer. There are of course alternative strategies available.

Essentially, these two prompts form a structured approach; the first prompt presents the problem and allows the model to produce a response, then the second prompt is presented, which allows the LLM to respond again. This second response is then checked for its answer. According to the APE paper, this format is prevalent. This makes it even more challenging to compare with zero-shot prompting where a simple 'please solve this problem' statement is made.

This two-prompt method is often referred to as a 'unit of evaluation'. They continue to evolve together; one mutation prompt goes hand-in-hand with one actual task prompt. This pairing isn't strictly necessary; the population of mutation prompts and task prompts could be kept separate. This combination is used because it is necessary to continuously evaluate the fitness of these elements. If you're familiar with evolutionary algorithms, you understand how this process is maintained; a population of these, assessed by their fitness level. Fitness levels are determined based on how accurate the prompts are. The mutation prompt, however, is slightly more complicated. Its evaluation is carried out in part due to having these aspects coupled. It's a lot easier to assess whether the prompts were useful based on their accuracy, as without the mutation prompt, they wouldn't have been generated.

It's feasible to check if the newly mutated prompts are more accurate than the previous prompts. However, in essence, the prompts and mutation prompts are kept together because the mutation prompts must be evaluated. They are assessed based on the accuracy of the prompts they produce. While not strictly necessary, from an engineering perspective, this method is utilized. This is why you will often see in the population that each individual consists of a prompt and a mutation prompt, or alternatively two prompts, and a mutation prompt, each of which possesses a fitness level.

As the algorithm progresses, this population is nurtured and evaluated. The individuals are ordered by fitness level and those with a low fitness are replaced with others that have been adapted from the fittest individuals in the population. This evolution-inspired process is how the algorithm progresses, consistently taking the fittest prompts, mutating them, and reintroducing them back into the population. Subsequently, every prompt and mutation prompt is ordered by fitness, every individual is evaluated, and those with the lowest fitness are replaced. This is the foundation of evolutionary algorithms.

Population-based Algorithms and Mutation Operators | 0:21:00-0:28:40

https://youtu.be/tkX0EfNl4Fc?t=1260

Population-based algorithms utilize mutation operators to alter prompts with the aim of evolving and improving them. These mutation operators can take an existing prompt and transform it into a new one, or they can generate an entirely new prompt from scratch. In this process, the unit of evolution is the prompt itself, which becomes transformed into a new prompt through mutation. Mutation prompts are essential to this procedure; they facilitate the generation of new prompts and evolution of current ones.

Hence, in such a scenario, the mutation prompt pair would indeed be transferred into the same mutation p' pair. It's also feasible to take a mutation prompt, create a new mutation prompt, which you can then use to mutate the original prompt into a new one. That's how they alter this population - they list those steps process down. They mention having nine operators for mutation. The reason for using this diverse set of operators is to allow the Language Learning Model (LLM) to explore a large space of cognitive methods of linguistic self-questioning, repeatedly altering the problem framing. At the same time, it aids in retrieving mental models expressed in natural language to help address a given reasoning challenge. Mutation operators will be discussed further.

In every round, the goal is to modify the population by mutating a set of individuals. In this ongoing process, individuals are reintroduced into the population based on fitness ordering, and those at the bottom are removed.

The mutation pertains to prompts, but also to the mutation prompts which are occasionally used to mutate the prompts. Direct mutation deals with generating a new task prompt, aka, zeroth-order generation. Here, we generate a new task by joining the problem's description with a list of 100 hints. This technique is applied right from the beginning when the initial list of prompts is created, ensuring that there's always a mechanism to generate prompts from the initial problem description. We avoid reaching a stage where we lose relevance to the original problem, which could be a degenerate state. The problem's description is the base for regeneration each time, where new prompts are generated and added without the use of any existing prompt or mutation prompt.

Then comes first-order prompt generation. Here, the process concatenates the mutation prompt with the parent task prompt and feeds it into the LLM to produce a mutated task prompt. For instance, the mutation prompt might say, "Rephrase this instruction in another way and avoid using any words from the original instruction." Given that, the instruction could be, "Solve the math word problem and present your answer as an Arabic numeral." This is a classic example of how mutation prompts and prompts interact, leading to the generation of a new prompt. The process is almost identical to the initialization method except for the non-utilization of a randomly sampled thinking style string.

The aim of this paper is rather hands-off, avoiding the need for manual engineering pertaining to this prompting process. However, many aspects of this paper are clearly based on trial and error, discovering what works best, the usage of "thinking styles" is a perfect example. Therefore, while they aim for a general approach, specific tweaks and operators are, in fact, created as a result of trial and error. As a result, the problem is managed rather than solved, it's simply shifted to a domain of meta-prompting. It's like teaching a person how to fish instead of simply providing them with a fish, but it's overly focused on a specific fishing method in a particular pond with a certain fishing line. Plus, the fact that all this utilizes training data contradicts the principle of working with LLMs.

Conditioning on Parents for Task Prompt Generation | 0:28:40-0:36:20

https://youtu.be/tkX0EfNl4Fc?t=1720

So, they have proposed, for instance, that one cannot merely condition on one parent, but rather on a set of parents. Accordingly, we supply a pruned and enumerated list of extant task prompts to the LLM, requesting it to extend the list with fresh task prompts. They simply aim to traverse through all their mutation units, they literally pass through all of these. They constantly extract only the prompts from each unit, arranged by their fitness level. Thus, they possess a list arranged in order of fitness and propose that they could just let the model continue that list. Yet, they strain it to eliminate items too similar; if too alike, based on cosine similarities, they are discarded. This sort of stipulates a diverse list, promoting diversity.

However, I misspoke earlier. This specific mutation operator doesn't offer an ordered list but rather an unordered one that emphasizes diversity by eliminating overly similar elements. The subsequent one provides an ordered list of the same elements. This is a version of the prior, where task prompts are listed in order of fitness.

Initial experiments suggested that the LLM is more likely to create entries resembling those appearing later in the list, so the task prompts in the population are arranged in ascending order of fitness. The ones with the highest fitness are at the end of the list. Here, they deceive the LLM by stating that this is a list of responses in descending order of fitness, despite arranging it in ascending order. They argue this approach improves the diversity of sampling since, otherwise, it is overly biased towards producing a novel entry very similar to the last one. This seemingly contradictory tactic surprisingly appears to enhance the diversity of sampling. This, to me, is the most shocking example of employing quirky tricks to improve the score. Although I genuinely don't object to using these tricks and understand that they can improve the score, I believe it detracts from the value of this paper, which ostensibly advocates for a hands-off, automated system, dismissing handcrafted methods.

Moving forward, they discuss a lineage-based mutation, providing a unit of evolution with the history of the individuals in its lineage. This shows how the unit evolved over time; it was mutated and continued to survive in the population, indicating its fitness probably increased. They asked if the LLM could extend that list and thereby improve it. They provided it in chronological order, which, given the evolutionary algorithm, most likely represents ascending quality. The same approach isn't used for all units, only where it proved beneficial on their specific problem with their particular method.

They then address hypermutation, describing how mutation prompts themselves can be mutated. They employ a "zeroth order" prompt mutation, where they append a randomly selected "thinking style" to the original problem description and ask the LLM to come up with a fresh mutation prompt. Once more, it's uncertain why "thinking styles" are employed; perhaps simply because it worked better. Likewise, "first order" hypermutation involves appending a hypermutation prompt to a mutation prompt, again resulting in a new mutation prompt. Despite being quite generic, it remains a handcrafted prompt. They also introduce Lamarckian evolution, where they draw on a collection of prior examples to guide a new prompt. Additionally, they use other familiar tactics from the field of evolutionary algorithms, such as prompt crossover and context shuffling.

PromptBreeder Strategy | 0:36:20-10:10:10

https://youtu.be/tkX0EfNl4Fc?t=2180

Their results are that they exceed other automated prompt generation methods and outperform hand-designed prompts. They assert this claim in the context of a particular classification problem, which is the detection of hate speech.

The strategy used by PromptBreeder involves two sophisticated prompts that yield a score of 89%. This score signifies an enhancement over a hand-designed prompt for identifying hate speech, which scores 80%. It's worth noting that the manually crafted prompt can yield 80% accuracy in under 30 seconds without any preceding training data. To reach an accuracy of 89%, the strategy incorporates training data and dataset information into the process.

Challenges including data gathering and implementing two consecutively issued promptsΓÇöone of which is crafted by an evolutionary algorithms exist. Yet, I believe such a strategy could be utilized in various tasks within the identical meta-domain.

One could ponder what a human could accomplish within just 15 minutes. The developed mutation prompts are noteworthy, with the top-rated one being "please summarize and improve the following instruction." This is the most successful mutation prompt evolved reflexively. The fact that the highest-scoring mutation prompt is successful essentially highlights what one would initially conceive. It's compelling, but does this fully justify such complexity? Notably, the most potent mutation operators are the 0th order hypermutation, where a new mutation prompt is simply devised.

The lack of a dominant mutation operator is brought to light, suggesting all operators contribute constructively. The core concept of first-order hypermutation, where a mutation prompt modifies a task prompt, is vital. The research underscores the prominence of evolved contexts in few-shot evolution, stressing the use of in-domain training data to achieve superior results.

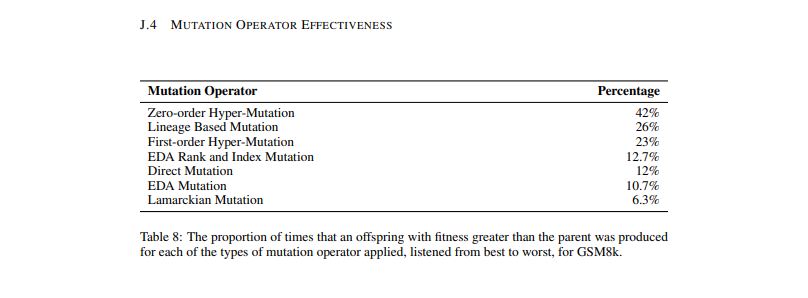
The concept of solving math word problems without a calculator captivates me as both intriguing and practical. However, I am unsure if this is the optimal prompt for self-assessment. I question whether the conclusions are genuinely sensible or swayed by external factors. Despite my uncertainties, I recognize the merit of this research and eagerly anticipate future advancements.

Promptbreeder: Self-Referential Self-Improvement Via Prompt Evolution (Paper Explained)

Affiliate Marketing